Herbstliche Mathematik

[ottogal]

Hallo in die Runde!

Das noch herumliegende Herbstlaub soll doch endlich entsorgt werden.
Mit dem Placet von Rolf löse ich hiermit auf:

---

Behauptung:

Der gesuchte Winkel $$\angle{BFE}$$ hat 45°, unabhängig vom Verhältnis der Radien der Viertelkreise.

Begründung:

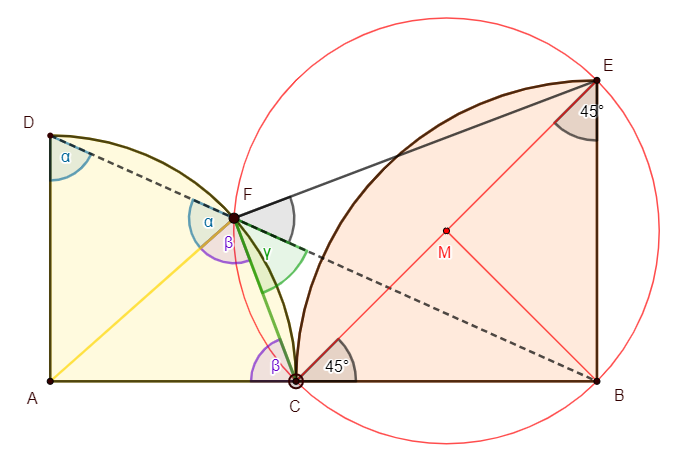
Sei F der Schnittpunkt von DB mit dem linken Viertelkreis.

Da AF ein Radius des linken Viertelkreises ist, sind die Dreiecke FDA und CFA gleichschenklig mit den Basiswinkeln $$\alpha$$ bzw. $$\beta$$.

Für die Winkelsumme im Viereck ACFD gilt

$$90°+2\beta+2\alpha=360°$$, also

$$\alpha+\beta=135°$$.

Wir erhalten $$\gamma=\angle{CFB}=180°-(\alpha+\beta)=45°$$.

Der rote Kreis ist der Umkreis k des gleichschenklig-rechtwinkligen Dreiecks ECB.
$$\angle{CEB}=45°$$ ist Umfangswinkel zur Sehne CB im Kreis k.
Da nun auch $$\gamma=\angle{CFB}=45°$$ ist, muss nach der Umkehrung des Umfangswinkel-Satzes auch F auf k liegen.

Nach Thales ist somit $$\angle{CEF}=90°$$, und man erhält den gesuchten Winkel
$$\angle{BFE}= 90°-\gamma=45°$$.

q.e.d.

---