Herbstliche Mathematik

[ottogal]

Also weiß man, dass der UWS hier auch gelten muss.

So kann mans nicht ausdrücken. Es geht um die Anwendung der Umkehrung des Umfangswinkelsatzes.
(Allgemein:
Lautet ein Satz: "Aus Aussage A folgt Aussage B",
dann lautet seine Umkehrung: "Aus Aussage B folgt Aussage A".)

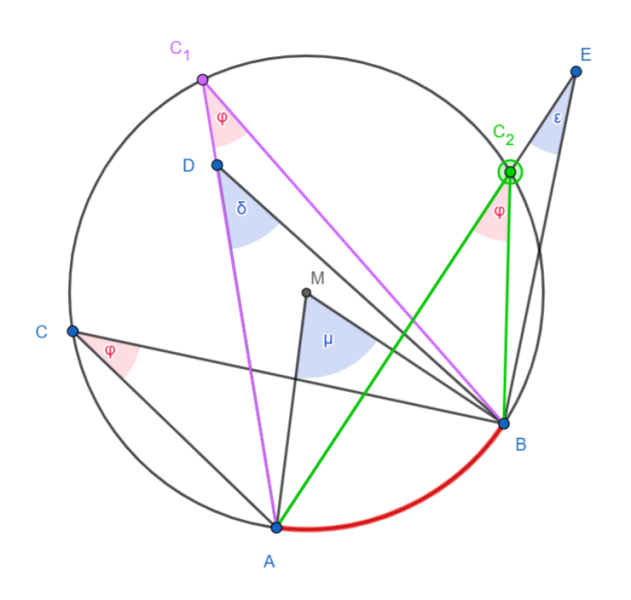
Nach dem Kreiswinkelsatz ist der Umfangswinkel $$φ=\angle{ACB}$$ zu einem bestimmten Kreisbogen (AB) stets halb so groß wie der zu diesem gehörende Mittelpunktswinkel $$μ=\angle{AMB}$$.
Verschiebt man also C auf dem nicht-roten Teil des Kreises, so bleibt der $$\angle{ACB}$$ stets gleich.
(Das ist der Umfangswinkelsatz.)

Daraus folgt: Ist D ein Punkt innerhalb des Kreises, so ist der $$δ=\angle{ADB}$$ stets größer als φ.
Nimmt man nämlich $$C_1$$ als Schnittpunkt von AD mit dem Kreis, so ist δ um den spitzen $$\angle{C_1BD}$$ größer als φ (Stichwort: Außenwinkelsatz!).

Entsprechendes gilt für einen Punkt E außerhalb des Kreises. Hier ist $$ε=\angle{AEB}$$ um den spitzen $$\angle{EBC_2}$$ kleiner als φ .

Aus diesen Überlegungen folgt nun: Ist P ein Punkt mit $$\angle{APB}=φ$$, so muss er auf dem Kreis liegen.
(Das ist die Umkehrung des Umfangswinkelsatzes.)