Funktion zur Berechnung zufälliger Bewegungen

[var]

Hallo miteinander!

Ich beschäftige mich seit einiger Zeit mit der Grafikprogrammierung im Kontext von WebGL und in diesem Zusammenhang begegnete mir zuletzt immer häufiger ein Problem, für das ich leider noch keine wirklich überzeugende Lösung gefunden habe, weil ich dabei irgendwie auf dem Schlauch stehe, weshalb ich mich in dieser Sache nun hoffnungsvoll an euch wende. ;-)

Grob gesagt, geht es dabei um die funktionale Beschreibung zufälliger Bewegungsmuster im dreidimensionalen Raum und innerhalb bestimmter Parameter.

Statt nun viele Worte zu verlieren, habe ich den Gegenstand der Problematik einmal in WebGL schematisch visualisiert, wobei die willkürliche Bewegung durch NURBS-Kurven symbolisiert wird und der Parameter Bewegungsradius als Sphere dargestellt ist:

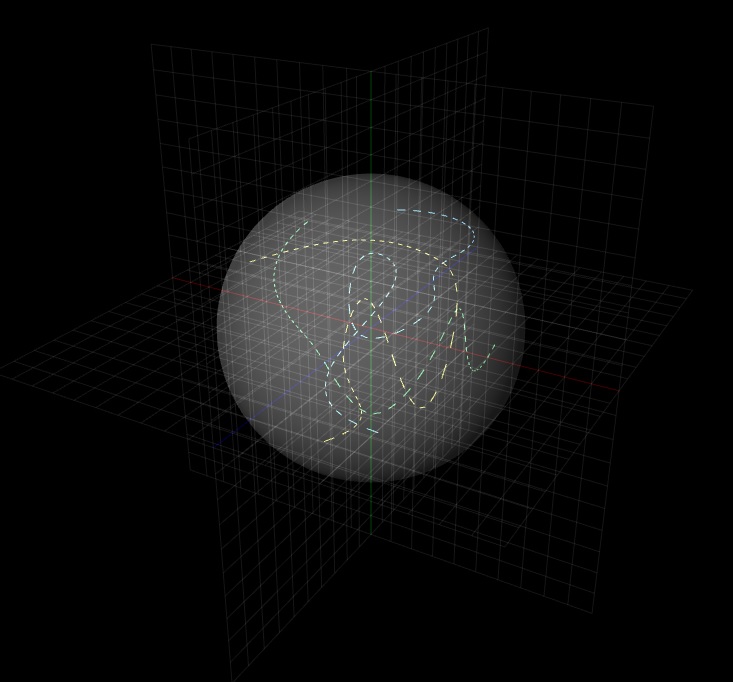
Die Funktion, die ich versuche zu schreiben, soll demnach ausgehend von gewissen Parametern eine zufällige Flugbahn eines Objektes berechnen, wobei als Parameter zunächst einmal der Startpunkt der Bewegung und die dabei maximal erreichbare Entfernung von einem bestimmten Punkt im kartesischen Koordinatensystem, also der Bewegungsradius, anzugeben ist.

Auch die Geschwindigkeit der Bewegung, beziehungsweise - als Option - die diesbezügliche Angabe eines Minimal- und eines Maximalwertes, innerhalb derer die Geschwindigkeit zufällig variieren kann, sollte natürlich festgelegt werden können, sowie - optional - ein zeitlicher Endpunkt der Animation, an dem die Startkoordinaten wieder erreicht werden und ein neuer Iterationszyklus beginnen kann.

Schließlich sollte auch eine zufällige Eigenrotation des Objektes hinzugefügt werden können.

Die einzelnen Transformationen werden dabei freilich durch Matrixberechnungen vollzogen, das heißt, durch Manipulation der quadratischen Matrix, welche das zu bewegende Objekt repräsentiert und die an Stelle der Originalkoordinaten ebenfalls als Parameter zu übergeben ist.

Die Funktionen zur Erstellung einer Einheitsmatrix sowie zu deren Translation und Rotation habe ich schon geschrieben, sowohl in JavaScript als auch in GLSL, und auch Funktionen zur Interpolation mittels quadratischer oder kubischer Bezierkurven oder durch B-Splines / NURBS stünden theoretisch zur Verfügung, das heißt dieser Teil der Lösung ist soweit gegeben...

var modelMatrix = createMat4( ); // returns identity mat4

translateMat4( modelMatrix, [x, y, z] ); // mat4, vec3

rotateMat4( modelMatrix, [x, y, z], angle ); // mat4, vec3, float

...bloß die restlichen Teile sinnvoll zusammenzufügen - was das angeht, da bin ich irgendwie blockiert, obwohl man meinen sollte, dass die Umsetzung nicht allzu schwierig wäre!

Der Sinn und Zweck des Ganzen liegt dabei jedenfalls - zumindest momentan - nicht nur darin begründet, tatsächlich zu rendernde 3D-Objekte zu animieren, sondern vor allem darin, Kamerafahrten in abstrakten Geometrien wie beispielsweise Fraktalen zu beschreiben, bei denen sich anders als in gegenständlichen Szenen die Kameraposition nicht direkt aus dem darzustellenden Inhalt selbst heraus bedingt.

In solchen Fällen habe ich bislang immer nur mehr oder weniger individuelle Lösungen mit recht bescheidener Funktionalität geschrieben, was irgendwie unbefriedigend war, weshalb mir eine generalisierte Funktion hier ziemlich erstrebenswert erscheint.

Naja, wie auch immer, jedenfalls wäre ich für jede Hilfe dankbar! ;-)

Beste Grüße,

var ♂

[Gunnar Bittersmann]

@@var

Die Funktion, die ich versuche zu schreiben, soll demnach ausgehend von gewissen Parametern eine zufällige Flugbahn eines Objektes berechnen

Sowas wie die Brownsche Molekularbewegung?

Auch die Geschwindigkeit der Bewegung, beziehungsweise - als Option - die diesbezügliche Angabe eines Minimal- und eines Maximalwertes, innerhalb derer die Geschwindigkeit zufällig variieren kann, sollte natürlich festgelegt werden können,

Ich würde denken, die Beschleunigung variiert zufällig. Höchst unwahrscheinlich, dass die Geschwindigkeit von einem Iterationsschritt zum nächsten bspw. auf $$\vec v_{n+1}=-\vec v_n$$ springt.

Und da wäre wohl in Polarkoordinaten zu rechnen: Die Richtungsänderung wäre gleichverteilt, der Betrag der Beschleunigung invers-normal-verteilt?

sowie - optional - ein zeitlicher Endpunkt der Animation, an dem die Startkoordinaten wieder erreicht werden und ein neuer Iterationszyklus beginnen kann.

Bei einer zufälligen Bewegung wird äußerst unwahrscheinlich der Ausgangszustand (selber Ort und selbe Geschwindigkeit (vektoriell)) wieder erreicht werden.

LLAP 🖖

[var]

Hallo Gunnar

Sowas wie die Brownsche Molekularbewegung?

Beim ersten Überfliegen scheint das jedenfalls ein interessanter Ansatz zu sein, vielen Dank für den Tip!

Mein bisheriges Konzept basierte darauf, aus der Menge der erlaubten Koordinatenwerte (begreunzt durch den zuvor definierten Bewegungsradius) Zufallspunkte auszuwählen und die Wegstrecke mittels NURBS zu interpolieren, wobei man dann durch entsprechende Parametrisierung der Wichtung Einfluss auf die Stetigkeit der Bewegungskurven nehmen konnte.

Ich würde denken, die Beschleunigung variiert zufällig. Höchst unwahrscheinlich, dass die Geschwindigkeit von einem Iterationsschritt zum nächsten bspw. auf $$\vec v_{n+1}=-\vec v_n$$ springt.

Präzise ausgedrückt, ja.

Für Kamerafahrten ist es vielleicht gar nicht so sinnvoll, wenn sich Geschwindigkeit und Eigenrotation der Kamera ständig ändern, sondern die Kamera einen zufälligen Impuls nach einem Zeitintervall erfährt, wobei die Länge der Zeitintervalle auch invers-normal-verteilt ist?

Ja, definitiv! Die Stetigkeit sowohl der Richtung als auch der Geschwindigkeit müssten natürlich in einer allgemein gefassten Funktion gesondert parametrisiert werden, sowohl für die Bewegung im Raum, als auch für die Eigenbewegung.

Bei einer zufälligen Bewegung wird äußerst unwahrscheinlich der Ausgangszustand (selber Ort und selbe Geschwindigkeit (vektoriell)) wieder erreicht werden.

Das ist richtig, aber gerade darin liegt, soweit ich das überblicke, der Charme der Spline-Interpolierung, da hier einfach nach einer bestimmten Zeit quasi manuell wieder Kurs gesetzt werden kann in Richtung Ausgangspunkt, ohne dass es dabei zwangsläufig zu einem Bruch kommt.

Hmmmmhhh... ich sehe schon, sobald man vom Konkreten zum Allgemeinen sich begibt, wird's kompliziert!

Jedenfalls habe ich jetzt einiges an Lektüre, nach der ich hoffentlich schlauer bin... ;-)

Nochmal vielen Dank für die Hinweise!

Gruß,

var ♂

[Gunnar Bittersmann]

@@var

Der Sinn und Zweck des Ganzen liegt dabei jedenfalls - zumindest momentan - nicht nur darin begründet, tatsächlich zu rendernde 3D-Objekte zu animieren, sondern vor allem darin, Kamerafahrten in abstrakten Geometrien wie beispielsweise Fraktalen zu beschreiben

Für Kamerafahrten ist es vielleicht gar nicht so sinnvoll, wenn sich Geschwindigkeit und Eigenrotation der Kamera ständig ändern, sondern die Kamera einen zufälligen Impuls nach einem Zeitintervall erfährt, wobei die Länge der Zeitintervalle auch invers-normal-verteilt ist?

LLAP 🖖