Mathematik zum Wochenende

[Gunnar Bittersmann]

@@Matthias Apsel

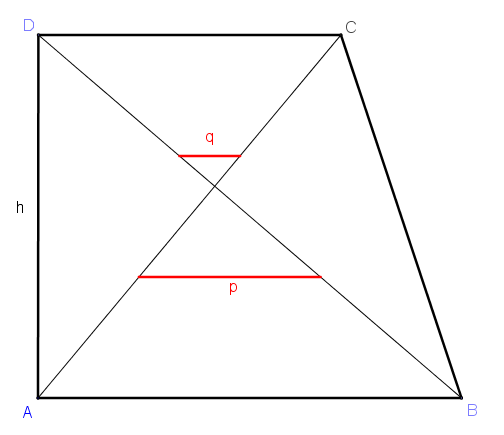
gegeben ist ein Trapez ABCD mit a || p || q || c, d(a, p) = d(p, q) = h/3

a) Berechne die Längen von p und q für a=7, c=5, h=6 und ⍺=90°.
b) Zeige, dass die Längen von p und q unabhängig von ⍺ sind.
c) Berechne die Längen von p und q für beliebiges a, c, h.

Wo das Wochenende nun vorbei ist, stelle ich mal meine Lösung vor:

Lege ein Koordinatensystem so, dass A in O liegt und a auf der positiven Seite der x-Achse.

(Die richtige Lage des Koordinatensystems ist das A und O bei der Lösung einer Aufgabe. ;-))

b) Die Änderung des Winkels ⍺ ist eine Scherung xʹ = x + my, yʹ = y.

Der Abstand zweier Punkte (x₁ʹ, yʹ) und (x₂ʹ, yʹ) auf einer horizontalen Linie ist
x₂ʹ − x₁ʹ = x₂ + my − x₁ − my = x₂ − x₁, also von m, d.h. auch von ⍺ unabhängig.

Da a, c, p und q horizontale Linien sind, sind p und q unabhängig von ⍺.

c) O.B.d.A. kann also davon ausgegangen werden, dass ⍺ rechtwinklig ist. D(0, h) liegt auf der y-Achse; die beiden anderen Eckpunkte haben die Koordinaten B(a, 0) und C(c, h).

Die Endpunkte von p und q seien P₁, P₂, Q₁, Q₂. Deren Koordinaten sind P₁(⅓c, ⅓h), P₂(⅔a, ⅓h), Q₁(⅓a, ⅔h), Q₂(⅔c, ⅔h).

Daraus ergibt sich p = |⅔a − ⅓c|, q = |⅔c − ⅓a|.

Anmerkung: Je nach Verhältnis von a : c können p und q auch auf derselben Seite des Schnittpunkts der Diagonalen liegen. Damit deren Werte nichtnegativ sind, die Absolutbeträge der Differenzen.

a) Ist mir jetzt zu blöd. ;-)

LLAP 🖖