Mathematik zum Wochenende

[Matthias Apsel]

Hallo alle,

gegeben ist ein Trapez ABCD mit a || p || q || c, d(a, p) = d(p, q) = h/3

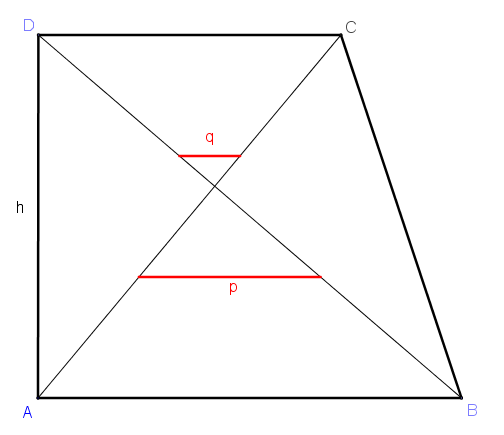
a) Berechne die Längen von p und q für a=7, c=5, h=6 und ⍺=90°.
b) Zeige, dass die Längen von p und q unabhängig von ⍺ sind.
c) Berechne die Längen von p und q für beliebiges a, c, h.

Bis demnächst
Matthias

[ottogal]

Ich rate mal: a = AB ? c = CD ? ⍺ = <BAD ?

[Matthias Apsel]

Hallo ottogal,

Ich rate mal: a = AB ? c = CD ? ⍺ = <BAD ?

Ja.

Bis demnächst
Matthias

[Rolf b]

Was soll man sich unter d(a,p) vorstellen?

[Matthias Apsel]

Hallo Rolf b,

Was soll man sich unter d(a,p) vorstellen?

d steht für distance. Damit ist der Abstand zwischen a und p gemeint.

Bis demnächst
Matthias

[Gunnar Bittersmann]

@@Matthias Apsel

gegeben ist ein Trapez ABCD mit a || p || q || c, d(a, p) = d(p, q) = h/3

a) Berechne die Längen von p und q für a=7, c=5, h=6 und ⍺=90°.
b) Zeige, dass die Längen von p und q unabhängig von ⍺ sind.
c) Berechne die Längen von p und q für beliebiges a, c, h.

Wo das Wochenende nun vorbei ist, stelle ich mal meine Lösung vor:

Lege ein Koordinatensystem so, dass A in O liegt und a auf der positiven Seite der x-Achse.

(Die richtige Lage des Koordinatensystems ist das A und O bei der Lösung einer Aufgabe. ;-))

b) Die Änderung des Winkels ⍺ ist eine Scherung xʹ = x + my, yʹ = y.

Der Abstand zweier Punkte (x₁ʹ, yʹ) und (x₂ʹ, yʹ) auf einer horizontalen Linie ist
x₂ʹ − x₁ʹ = x₂ + my − x₁ − my = x₂ − x₁, also von m, d.h. auch von ⍺ unabhängig.

Da a, c, p und q horizontale Linien sind, sind p und q unabhängig von ⍺.

c) O.B.d.A. kann also davon ausgegangen werden, dass ⍺ rechtwinklig ist. D(0, h) liegt auf der y-Achse; die beiden anderen Eckpunkte haben die Koordinaten B(a, 0) und C(c, h).

Die Endpunkte von p und q seien P₁, P₂, Q₁, Q₂. Deren Koordinaten sind P₁(⅓c, ⅓h), P₂(⅔a, ⅓h), Q₁(⅓a, ⅔h), Q₂(⅔c, ⅔h).

Daraus ergibt sich p = |⅔a − ⅓c|, q = |⅔c − ⅓a|.

Anmerkung: Je nach Verhältnis von a : c können p und q auch auf derselben Seite des Schnittpunkts der Diagonalen liegen. Damit deren Werte nichtnegativ sind, die Absolutbeträge der Differenzen.

a) Ist mir jetzt zu blöd. ;-)

LLAP 🖖

[Rolf b]

Hallo Gunnar,

sehr schön und kompakt. Ich habe Koordinaten ignoriert, bin über den Strahlensatz gegangen und habe fleißig Verhältnisse nachgerechnet. Das Ergebnis war das gleiche, nur der Weg deutlich länger (weil ich auch noch den Schnittpunkt M berücksichtigen musste).

Rolf

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Anmerkung: Je nach Verhältnis von a : c können p und q auch auf derselben Seite des Schnittpunkts der Diagonalen liegen.

Nachgerechnet: Das ist bei a : c > 2 und bei a : c < ½ der Fall.

Für a : c = 2 ist q = 0; für a : c = ½ ist p = 0.

LLAP 🖖

[ottogal]

Meine Lösung

Der Diagonalenschnittpunkt des Trapezes heiße S. Die Trapezhöhe durch S sei EF (E auf AB, F auf CD). Die Endpunkte von p seien G und H, der Schnittpunkt von GH mit EF heiße K. Die Endpunkte von q seien Q und P, der Schnittpunkt von QP mit EF heiße R.

Beweis von c):

Sämtliche im Folgenden verwendeten Verhältnis-Gleichheiten folgen aus den Strahlensätzen mit dem Zentrum S. Zur Abkürzung bezeichnen wir das Verhältnis c/a mit k.

Man erhält:

SF/SE = SC/SA = c/a = k

SF = k*SE

SE*(1+k) = h

SE = h/(1+k)

SK = SE - h/3 = h*(1/(1+k) - 1/3)

SK = h*(2-k) / 3*(1+k)

p/a = SG/SA = SK/SE = SK*(1/SE) = ((2-k) / 3*(1+k)) * (1+k)

p = a*(2-k)/3

Mit k = c/a wird daraus

p = (2*a - c)/3

Aus SF = k*SE folgt weiter:

SF= h*k/(1+k)

SR = SF - RF = h*( k/(1+k) - 1/3 )

SR = h*(2k-1) / 3(1+k)

q/c = PQ/CD = SP/SC = SR/SF = (2k-1)/3(1+k) / (1+k)/k = (2k-1) / 3k

q = c*(2k-1) / 3k = c*(2-1/k)/3

Mit 1/k = a/c wird daraus q = c*(2-a/c)/3, also

q = (2*c-a)/3

Zu a): Aus den gegebenen Daten erhält man mit den gefundenen Formeln p = 3 und q = 1.

Zu b): Alle im obigen Beweis verwendeten Verhältnis-Gleichheiten gelten unabhängig vom Winkel ⍺.

[ottogal]

(Edit: Ich habe bei den meisten Produkten den * für die Multiplikation weggelassen, da das hier manchmal automatisch geschieht. Konnte den vorherigen Post nicht mehr bearbeiten, kA weshalb.)

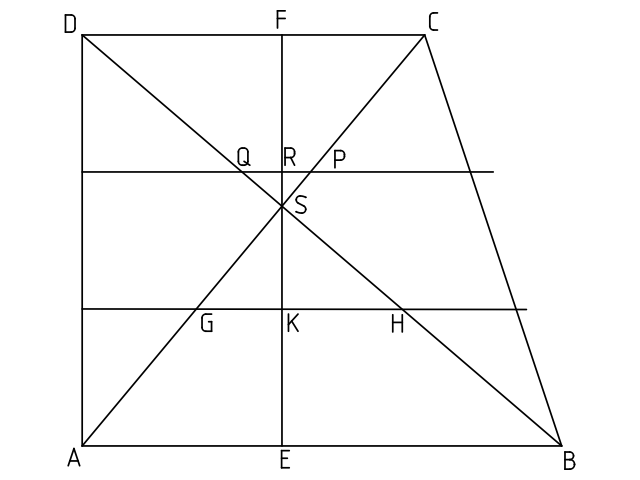
Meine Lösung

Der Diagonalenschnittpunkt des Trapezes heiße S. Die Trapezhöhe durch S sei EF (E auf AB, F auf CD). Die Endpunkte von p seien G und H, der Schnittpunkt von GH mit EF heiße K. Die Endpunkte von q seien Q und P, der Schnittpunkt von QP mit EF heiße R.

Beweis von c):

Sämtliche im Folgenden verwendeten Verhältnis-Gleichheiten folgen aus den Strahlensätzen mit dem Zentrum S. Zur Abkürzung bezeichnen wir das Verhältnis c/a mit k.

Man erhält:

SF/SE = SC/SA = c/a = k

SF = k SE

(1+k)SE = SE + SF = h

SE = h/(1+k)

SK = SE - h/3 = h( 1/(1+k) - 1/3 )

SK = h(2-k) / 3(1+k)

p/a = SG/SA = SK/SE = (1/SE) SK = (1+k)/h * (h(2-k) / 3(1+k)) = (2-k)/3

p = (2-k)a/3

Mit k = c/a wird daraus

p = (2a-c)/3

Aus SF = k SE folgt weiter:

SF= kh/(1+k)

SR = SF - RF = h( k/(1+k) - 1/3 )

SR = h*( 2k-1) / 3(1+k) )

q/c = PQ/CD = SP/SC = SR/SF = (2k-1)/3(1+k) / (1+k)/k = (2k-1) / 3k

q = c*(2k-1) / 3k = c*(2-1/k)/3

Mit 1/k = a/c wird daraus q = c*(2-a/c)/3, also

q = (2c-a)/3

Zu a): Aus den gegebenen Daten erhält man mit den gefundenen Formeln p = 3 und q = 1.

Zu b): Alle im obigen Beweis verwendeten Verhältnis-Gleichheiten gelten unabhängig vom Winkel ⍺.

[Gunnar Bittersmann]

@@ottogal

SK = SE - h/3

Nein, das dann man so nicht sagen. Das gilt nur dann, wenn K und E auf h auf derselben Seite von S liegen. Davon kannst du aber nicht ausgehen.

Wenn du o.B.d.A. a ≥ c annimmst, kannst du es.

SR = SF - RF

Nein, das dann man so nicht sagen. Das gilt nur dann, wenn R und F auf h auf derselben Seite von S liegen. Davon kannst du aber nicht ausgehen.

Die Beschränkung auf Parallelogramme wäre eine Beschränkung der Allgemeinheit.

Mit Betragsstrichen sollte es aber stimmen: SR = |SF − RF|

Die Betragsstriche musst du bis zum Ende deiner Rechung mitschleifen.

LLAP 🖖

[Matthias Apsel]

Hallo Gunnar Bittersmann,

Die Beschränkung auf Parallelogramme wäre eine Beschränkung der Allgemeinheit.

Imho nicht, weil der Strahlensatz sowohl für "Parallelogramme" im obigen Sinne, als auch für überschlagene Vierecke (ebenfalls im obigen Sinne) gilt.

Bis demnächst
Matthias

[Gunnar Bittersmann]

@@Matthias Apsel

SR = SF - RF

Die Beschränkung auf Parallelogramme wäre eine Beschränkung der Allgemeinheit.

Imho nicht, weil der Strahlensatz sowohl für "Parallelogramme" im obigen Sinne, als auch für überschlagene Vierecke (ebenfalls im obigen Sinne) gilt.

Das stimmt, aber darum ging es hier nicht. Hier geht’s nicht um Verhältnisse, sondern um die Differenz.

LLAP 🖖

[ottogal]

Wenn du o.B.d.A. a ≥ c annimmst, kannst du es.

Das habe ich in der Tat stillschweigend angenommen - hätte es freilich notieren müssen.

Die Beschränkung auf Parallelogramme wäre eine Beschränkung der Allgemeinheit.

War davon irgendwo die Rede?

Mit Betragsstrichen sollte es aber stimmen: SR = |SF − RF|

Yep.

Die Betragsstriche musst du bis zum Ende deiner Rechung mitschleifen.

Yo.

Danke!

P.S. Dieser Editor hier gibt mir Rätsel auf... (Kasten)

[Gunnar Bittersmann]

@@ottogal

Wenn du o.B.d.A. a ≥ c annimmst, kannst du es. […] Die Beschränkung auf Parallelogramme wäre eine Beschränkung der Allgemeinheit. War davon irgendwo die Rede?

Ich hatte dir mit „o.B.d.A. a ≥ c“ oben den Arsch gerettet. ;-)

Das war dann unten nicht mehr möglich gewesen, denn da hätte es zusätzlich „c ≥ a“ lauten müssen. Das hieße a = c; da isses, das Parallelogramm.

P.S. Dieser Editor hier gibt mir Rätsel auf... (Kasten)

| hat in Markdown eine Sonderbedeutung: Tabelle. Willst du ein | im Text verwenden, musst du es escapen: \|.

Ich hab das in deinem Posting mal berichtigt.

Wie hast du die \ wegbekommen? Ich hatte sie drin. Meinen Text (mit >  davor) übernehmen hätte sie drin gelassen.

LLAP 🖖

[ottogal]

Das war dann unten nicht mehr möglich gewesen, denn da hätte es zusätzlich „c ≥ a“ lauten müssen. Das hieße a = c; da isses, das Parallelogramm.

Ah ja, klar.

Wie hast du die \ wegbekommen? Ich hatte sie drin. Meinen Text (mit >  davor) übernehmen hätte sie drin gelassen.

Ich hatte deinen Text ohne das > kopiert und in ein leeres Zitat eingefügt.

[Gunnar Bittersmann]

@@ottogal

Das war dann unten nicht mehr möglich gewesen, denn da hätte es zusätzlich „c ≥ a“ lauten müssen. Das hieße a = c; da isses, das Parallelogramm.

Ah ja, klar.

BTW, es hätten auch die Bedingungen a > ½_c_ bzw. c > ½_a_ genügt. Was aber nichts daran ändert, dass ½_a_ < c < 2_a_ eine Beschränkung der Allgemeinheit wäre.

Wie hast du die \ wegbekommen? Ich hatte sie drin. Meinen Text (mit >  davor) übernehmen hätte sie drin gelassen.

Mit „übernehmen“ meinte ich natürlich „antworten“ (mit Zitat).

Ich hatte deinen Text ohne das > kopiert und in ein leeres Zitat eingefügt.

Dabei geht das Markdown natürlich verloren.

LLAP 🖖

[ottogal]

In meiner mit GeoGebra gefertigten dynamischen Zeichnung lassen sich die vier Ecken des Trapezes ABCD horizontal verschieben. So kann man schön die verschiedenen Fälle beobachten. (Z.B. fallen für c = 2a oder a = 2c jeweils drei der benannten Punkte mit S zusammen; denn dann ist p = 0 bzw. q = 0.)

[Gunnar Bittersmann]

@@ottogal

In meiner mit GeoGebra gefertigten dynamischen Zeichnung lassen sich die vier Ecken des Trapezes ABCD horizontal verschieben.

Sehr nett.

(Z.B. fallen für c = 2a oder a = 2c jeweils drei der benannten Punkte mit S zusammen; denn dann ist p = 0 bzw. q = 0.)

Das hatte ich auch schon nachgerechnet.

LLAP 🖖

[ottogal]

Verwendet man Vektoren, hat man das Problem mit der Fallunterscheidung bei Differenzen nicht. Freilich muss man am Ende beim Übergang zu den Streckenlängen wieder Betragstriche setzen - der Lorbeer gebührt hier Gunnar.

Der Beweis mit Vektoren:

Wegen der gleichen Abstände der Parallelen gilt

$$\vec{GC} = \frac{2}{3} \vec{AC}$$ und $$\vec{PC} = \frac{1}{3} \vec{AC}$$

Zur Abkürzung sei wieder $$k = \frac{c}{a}$$ gesetzt. Man erhält nacheinander:

$$\vec{SC} = k \cdot \vec{AS}$$

$$\vec{AC} = \vec{AS} + \vec{SC} = (1+k) \cdot \vec{AS}$$

$$\vec{SG} = \vec{SC} + \vec{CG} = k \cdot \vec{AS} - \frac{2}{3} \vec{AC} = k \cdot \vec{AS} - \frac{2}{3} \cdot (1+k) \cdot \vec{AS}$$

$$\vec{SG} = \frac{k-2}{3} \cdot \vec{AS}$$

$$\vec{SG} = \frac{2-k}{3} \cdot \vec{SA}$$

$$\vec{GH} = \frac{2-k}{3} \cdot \vec{AB}$$

$$p = \left| \frac{2-k}{3} \right| \cdot a$$

Mit $$k = \frac{c}{a}$$ folgt daraus

$$p = \left| \frac{2a - c}{3} \right|$$

Weiter gilt :

$$\vec{PC} = \frac{1}{3} \cdot (\vec{AS} + \vec{SC}) = \frac{1}{3} \cdot \left( \frac{1}{k} \vec{SC} + \vec{SC} \right) = \frac{1}{3} \cdot \left( \frac{1}{k} + 1 \right) \cdot \vec{SC}$$

$$\vec{PC} = \frac{1+k}{3k} \cdot \vec{SC}$$

$$\vec{SP} = \vec{SC} - \vec{PC} = \vec{SC} \cdot \left( 1 - \frac{1+k}{3k} \right)$$

$$\vec{SP} = \left( \frac{2k-1}{3k} \right) \cdot \vec{SC}$$

$$\vec{PQ} = \left( \frac{2k-1}{3k} \right) \cdot \vec{CD}$$

Wieder mit $$k = \frac{c}{a}$$ folgt

$$q = \left| \frac{2c - a}{3c} \right| \cdot c$$

$$q = \left| \frac{2c - a}{3} \right|$$

P.S. Übrigens sollte es nicht verwundern, dass die Ergebnisse für p und q nur von a und c, nicht aber von h abhängen: Es würde ja nichts an den Streckenverhältnissen ändern, würde man die vertikale Achse dehnen oder stauchen.

P.P.S. Das Markup hier hinzukriegen hat mich weit mehr Zeit gekostet als das ganze Beweisen. Zeit, mich wieder um wichtigere Dinge zu kümmern...