Lösung

[Gunnar Bittersmann]

@@Matthias Apsel

Ist ja rege Beteiligung hier. Da sich das Wochenende dem Ende neigt, präsentiere mal meinen Beweis. Gleich den für die allgemeine, oder wie Matthias sagte die Bittersmann-Variante:

b) - Die Bittersmann-Variante: Man beweise, dass das Dreieck MPQ stets rechtwinklig-gleichschenklig ist.

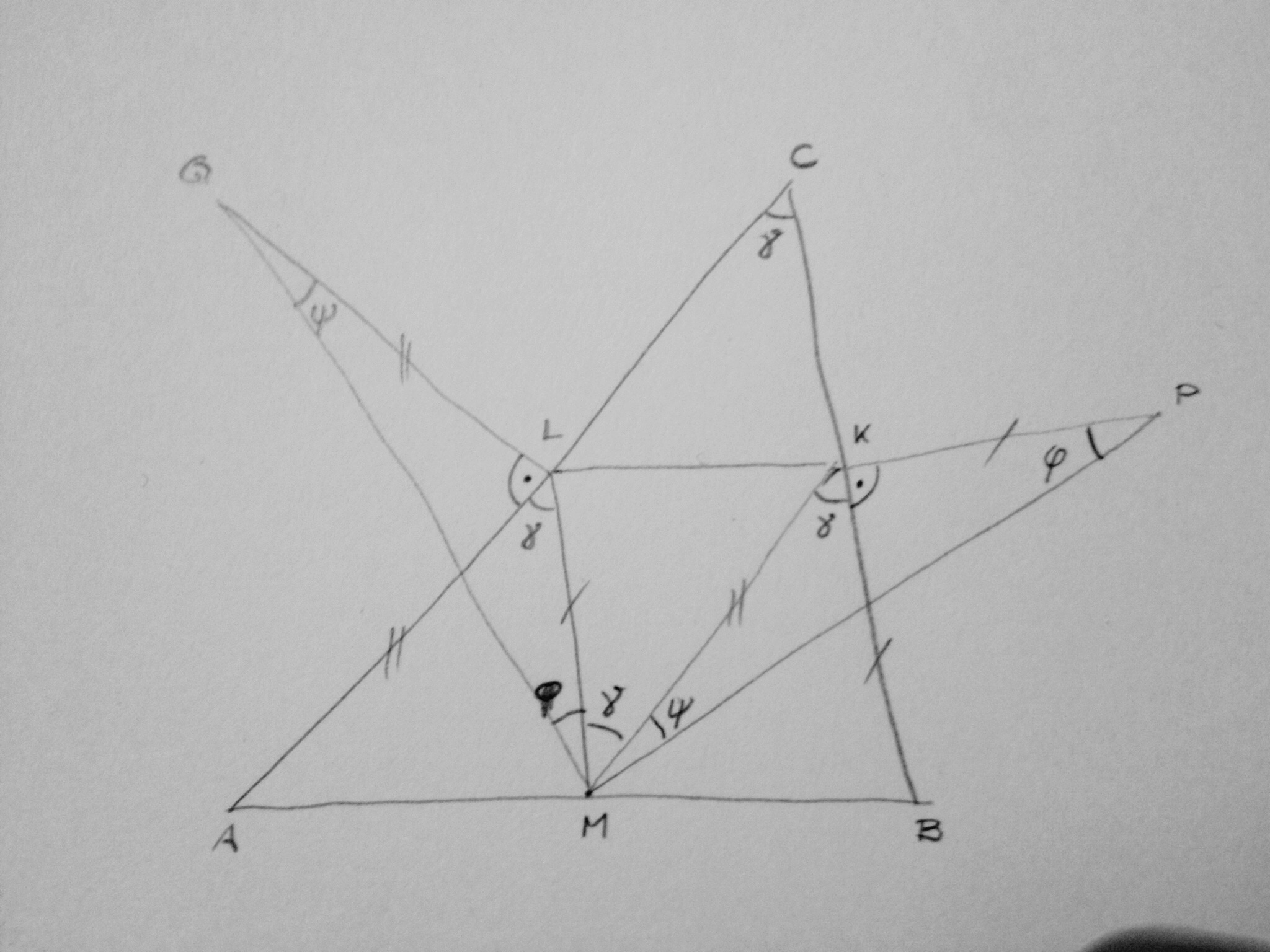
Seien M, K und L die Mittelpunkte der Seiten AB, BC und AC. Deren Verbindungen teilen das Dreieck ABC in vier kongruente Dreiecke. Es gilt ML = BK, MK = AL und ∠_MLA_ = ∠_BKM_ = ∠_LMK_ = γ.

Da das Dreieck BPC gleichschenklig sein soll, muss P auf der Mittelsenkrechten von BC durch K liegen. Da das Dreieck BPC gleichschenklig-rechtwinklig sein soll (mit rechtem Winkel bei P), muss auch das Dreieck BPK gleichschenklig-rechtwinklig sein (mit rechtem Winkel bei K), es gilt BK = KP.

Entsprechend liegt Q auf der Mittelsenkrechten von AC durch L, es gilt AL = LQ.

Damit gilt auch KP = ML und MK = LQ. Außerdem ist ∠_PKM_ = ∠_MLQ_ = γ + 1∟. Damit sind die Dreiecke MPK und MLQ kongruent, woraus MP = MQ folgt. Das Dreieck MPQ ist somit gleichschenklig.

Desweiteren folgt ∠_MPK_ = ∠_QML_ = φ sowie ∠_KMP_ = ∠_LQM_ = ψ. Wegen der Innenwinkelsumme im Dreieck MPK (bzw. MLQ) gilt φ + ψ + γ + 1∟ = 2∟, folglich φ + ψ + γ = 1∟.

Nun ist ebenfalls ∠_QMP_ = φ + ψ + γ = 1∟, das Dreieck MPQ ist somit rechtwinklig.

LLAP 🖖