Mathematik zum Wochenende

[Matthias Apsel]

Hallo alle!

Gegeben ist ein Dreieck ABC. Über zwei Dreiecksseiten werden rechtwinklig-gleichschenklige Dreiecke errichtet, und zwar so, dass die entsprechende Seite des Dreiecks ABC die Hypotenuse ist. Die beiden neuen Eckpunkte heißen P beziehungsweise Q. Der Mittelpunkt der dritten Seite des Dreiecks ABC wird mit M bezeichnet.

0. Man fertige eine Skizze an, ohne auf meine dynamische Vorarbeit zu schauen.

a) Man beweise, dass das Dreieck MPQ rechtwinklig-gleichschenklig ist, falls das Dreieck ABC rechtwinklig-gleichschenklig ist.

b) - Die Bittersmann-Variante: Man beweise, dass das Dreieck MPQ stets rechtwinklig-gleichschenklig ist.

Bis demnächst
Matthias

[Gunnar Bittersmann]

@@Matthias Apsel

Ich hab mal alle $$ durch _ ersetzt; LaTeX braucht man hier nicht. (Großbuchstaben aber. ;-))

b) - Die Bittersmann-Variante: Man beweise, dass das Dreieck MPQ stets rechtwinklig-gleichschenklig ist.

Hab’s. Und was soll ich jetzt am Wochenende tun?

LLAP 🖖

[Matthias Apsel]

Hallo Gunnar Bittersmann,

Ich hab mal alle $$ durch _ ersetzt; LaTeX braucht man hier nicht. (Großbuchstaben aber. ;-))

Ich finde den Font so ästhetisch.

b) - Die Bittersmann-Variante: Man beweise, dass das Dreieck MPQ stets rechtwinklig-gleichschenklig ist.

Hab’s. Und was soll ich jetzt am Wochenende tun?

Alle meine Beiträge positiv bewerten?

Bis demnächst
Matthias

[Gunnar Bittersmann]

@@Matthias Apsel

Ich hab mal alle $$ durch _ ersetzt; LaTeX braucht man hier nicht. (Großbuchstaben aber. ;-))

Ich finde den Font so ästhetisch.

Deshalb FOUT für alle?

Stell dir doch Serifenschrift ein.

Hab’s. Und was soll ich jetzt am Wochenende tun?

Alle meine Beiträge positiv bewerten?

Netter Versuch.

Du willst auch Moderator-Rechte haben? ;-)

LLAP 🖖

[Gunnar Bittersmann]

@@Matthias Apsel

Ist ja rege Beteiligung hier. Da sich das Wochenende dem Ende neigt, präsentiere mal meinen Beweis. Gleich den für die allgemeine, oder wie Matthias sagte die Bittersmann-Variante:

b) - Die Bittersmann-Variante: Man beweise, dass das Dreieck MPQ stets rechtwinklig-gleichschenklig ist.

Seien M, K und L die Mittelpunkte der Seiten AB, BC und AC. Deren Verbindungen teilen das Dreieck ABC in vier kongruente Dreiecke. Es gilt ML = BK, MK = AL und ∠_MLA_ = ∠_BKM_ = ∠_LMK_ = γ.

Da das Dreieck BPC gleichschenklig sein soll, muss P auf der Mittelsenkrechten von BC durch K liegen. Da das Dreieck BPC gleichschenklig-rechtwinklig sein soll (mit rechtem Winkel bei P), muss auch das Dreieck BPK gleichschenklig-rechtwinklig sein (mit rechtem Winkel bei K), es gilt BK = KP.

Entsprechend liegt Q auf der Mittelsenkrechten von AC durch L, es gilt AL = LQ.

Damit gilt auch KP = ML und MK = LQ. Außerdem ist ∠_PKM_ = ∠_MLQ_ = γ + 1∟. Damit sind die Dreiecke MPK und MLQ kongruent, woraus MP = MQ folgt. Das Dreieck MPQ ist somit gleichschenklig.

Desweiteren folgt ∠_MPK_ = ∠_QML_ = φ sowie ∠_KMP_ = ∠_LQM_ = ψ. Wegen der Innenwinkelsumme im Dreieck MPK (bzw. MLQ) gilt φ + ψ + γ + 1∟ = 2∟, folglich φ + ψ + γ = 1∟.

Nun ist ebenfalls ∠_QMP_ = φ + ψ + γ = 1∟, das Dreieck MPQ ist somit rechtwinklig.

LLAP 🖖

[Matthias Apsel]

Hallo Gunnar Bittersmann,

Respekt!

Bis demnächst
Matthias

[Matthias Apsel]

Hallo Gunnar Bittersmann,

Ist ja rege Beteiligung hier.

Ja. Leider. Woran lags? Ich glaube nicht, dass die speziellen Varianten zu schwer waren. Und Weihnachtsmärkte haben doch auch noch nicht geöffnet. Das Oktoberfest ist vorbei, der Martinimarkt steht noch aus.

Bis demnächst
Matthias

[MudGuard]

Hi,

Ja. Leider. Woran lags?

am genial schönen Wetter.

Ich hab das gestern genutzt, um den Forstenrieder Park von einem Teil seines Pilzbefalls zu befreien (Parasole, Safranschirmlinge, Maronen, Blaustiele, Nebelgraue Trichterlinge).

Und heute war ein entbeerungsreicher Tag: ich hab das Königsdorfer Moor stellenweise entbeert. Das gibt dann lecker Moosbeerln-Marmelade (nach EU-Ansicht: Konfitüre).

cu,
Andreas a/k/a MudGuard

[Matthias Apsel]

Hallo MudGuard,

am genial schönen Wetter.

Ich habe schon gehört, dass die Elbe heute eine Wetterscheide war.

Bis demnächst
Matthias

[Der Martin]

Hallo,

Ja. Leider. Woran lags?

für mich am Thema der Frage, das mich überhaupt nicht angesprochen hat.

am genial schönen Wetter.

Auch ein gutes Argument! Aber nicht für gestern, oder? Zumindest hier im Stuttgarter Raum war's gestern eher kühl und trüb, heute dafür nochmal ein Aufbäumen des Sommers mit blauem Himmel und Temperaturen über 20°C.

Ich hab das gestern genutzt, um den Forstenrieder Park von einem Teil seines Pilzbefalls zu befreien (Parasole, Safranschirmlinge, Maronen, Blaustiele, Nebelgraue Trichterlinge).

Von den genannten sind mir nur Parasol (aka Schirmpilz) und Maronen geläufig. Lecker! In einigen Waldstücken hier in der Region gedeiht auch der Hallimasch quasi wie Unkraut.

Leider hat das mit dem Entpilzen für mich inzwischen zwei Hürden: Erstens fällt es mir aus eigenem Antrieb schwer, überhaupt in den Wald zu gehen (ich empfinde Wald als etwas Düsteres, Bedrohliches, Schmutziges); zweitens wüsste ich im Erfolgsfall nicht, wie ich die Beute dann zubereiten muss.

Dafür hatte ich heute ein leckeres Abendessen, eine Art Experimentiersalat: Eine Paprikaschote, eine halbe Zwiebel, zwei Tomaten, ein paar Gewürzgurken kleingeschnibbelt und vermischt, dann noch ein paar Würfel Feta-Käse und eine kleine Dose Thunfisch dazu. Das Dressing ergab sich wie von selbst aus etwas Gurkenbrühe und ein bisschen von dem Sonnenblumenöl, in dem der Thunfisch gewohnt hat. Mmmh ...

Und heute war ein entbeerungsreicher Tag: ich hab das Königsdorfer Moor stellenweise entbeert.

*fg*

So long,
 Martin

[MudGuard]

Hi,

am genial schönen Wetter.

Auch ein gutes Argument! Aber nicht für gestern, oder?

Doch, hier im Süden Münchens schon. Ok, Spätnachmittag hat's etwas zugezogen ...

Ich hab das gestern genutzt, um den Forstenrieder Park von einem Teil seines Pilzbefalls zu befreien (Parasole, Safranschirmlinge, Maronen, Blaustiele, Nebelgraue Trichterlinge).

Von den genannten sind mir nur Parasol (aka Schirmpilz) und Maronen geläufig. Lecker! In einigen Waldstücken hier in der Region gedeiht auch der Hallimasch quasi wie Unkraut.

Safranschirmling: ist ein kleinerer Pilz aus der Familie der Schirmlinge (zu denen auch der Parasol zählt). Sieht wie eine kleinere Version des Parasol aus, aber eher weißlich und weniger bräunlich. Beim Anschneiden/Brechen färbt sich die Stelle gelblich (safran-farben), später rötlich.

Blaustiel: Blätterpilz, oben bräunlich, untendrunter blau bis milka-lila. Ältere Exemplare auch auf der Oberseite am Rand lila. Wegen der Kombination von braun und lila wurde der Pilz auch schon als "Milka-Pilz" bezeichnet (von einer damals ca. 5-jährigen).

Nebelgrauer Trichterling: jung obendrauf dunkelgrau, ältere gröpere Exemplare hellgrau und mit trichterförmigem Hut, die Blätter weiß bis creme-farben. Kann bei empfindlichen Personen zu Durchfall führen, wenn größere Mengen gegessen werden.

Leider hat das mit dem Entpilzen für mich inzwischen zwei Hürden: Erstens fällt es mir aus eigenem Antrieb schwer, überhaupt in den Wald zu gehen (ich empfinde Wald als etwas Düsteres, Bedrohliches, Schmutziges);

Da kann ich nicht helfen.

zweitens wüsste ich im Erfolgsfall nicht, wie ich die Beute dann zubereiten muss.

Parasol: Stiel durch Drehen entfernen, Hut vierteln, das Zentrum (da, wo der Stiel drunter war) entfernen. Butter in der Pfanne erhitzen, Hut-Teile reingeben und von beiden Seiten braun braten. Salzen, pfeffern, genießen.

Seeeeehr lecker!

Ersatzweise, wenn man auf Panade steht: vor dem Braten panieren.

---

gemischte Pilze: Zwiebel schälen, würfeln, in Butter bei mittlerer Temperatur leicht glasig werden lassen. Die in Stücke geschnittenen Pilzen dazugeben. Beim Braten entsteht nach einiger Zeit in der Pfanne Flüssigkeit (die aus den Pilzen kommt). Weiterbraten, bis die Flüssigkeit wieder weg ist. Ab hier zwei Möglichkeiten: Ei unterrühren oder Sahne. Salzen und Pfeffern.

Seeeehr lecker!

Dafür hatte ich heute ein leckeres Abendessen, eine Art Experimentiersalat: Eine Paprikaschote, eine halbe Zwiebel, zwei Tomaten, ein paar Gewürzgurken kleingeschnibbelt und vermischt, dann noch ein paar Würfel Feta-Käse und eine kleine Dose Thunfisch dazu. Das Dressing ergab sich wie von selbst aus etwas Gurkenbrühe und ein bisschen von dem Sonnenblumenöl, in dem der Thunfisch gewohnt hat. Mmmh ...

Und heute war ein entbeerungsreicher Tag: ich hab das Königsdorfer Moor stellenweise entbeert.

*fg*

So long,
 Martin

cu,
Andreas a/k/a MudGuard

[Tabellenkalk]

Hallo,

Forstenrieder Park von einem Teil seines Pilzbefalls zu befreien

Ich fürchte, du warst da nur oberflächlich tätig. Wenn du gründlich sein willst, musst du auch das Myzel mit entfernen :P

Gruß
Kalk

[MudGuard]

Hi,

Forstenrieder Park von einem Teil seines Pilzbefalls zu befreien

Ich fürchte, du warst da nur oberflächlich tätig.

ja, darum ja auch "von einem Teil".

Wenn du gründlich sein willst, musst du auch das Myzel mit entfernen :P

Ne, das will ich ja nicht, sonst kann ich ja nächste Saison nichts ernten ...

cu,
Andreas a/k/a MudGuard

[Rolf b]

Ein Dreieck lässt sich durch die Seitenmittelpunkte in 4 kongruente Teildreiecke aufteilen. AHA! Vielleicht mal gewusst, aber wenn, dann komplett verdrängt und jetzt auch nicht drauf gekommen. Ist natürlich sonnenklar, wenn man es sieht.

Und das war hier wohl der Schlüssel zum Erfolg. Ich habe ein paar frustrierende Stunden mit Sinus- und Cosinussatz verbracht, habe auch überlegt wo sich Strahlensätze verstecken (aber nicht hinreichend, sonst wäre ich ja auf die Teildreiecke gestoßen) und dann keine Lust mehr gehabt. Ob ich es geschafft hätte, wenn ich auf die Teildreiecke gestoßen wäre - keine Ahnung.

Um die Frage "zu schwer" zu klären, wäre es interessant gewesen, die kongruente Unterteilung als Tipp zu posten. Ich war allerdings gestern und heute zu 90% der Zeit außer Haus, ob ich dann noch Lust gehabt hätte kann ich jetzt auch nicht sagen.

Respekt @ Gunnar.

Gruß
Rolf

[Matthias Apsel]

Hallo Rolf b,

Ein Dreieck lässt sich durch die Seitenmittelpunkte in 4 kongruente Teildreiecke aufteilen. AHA! Vielleicht mal gewusst, aber wenn, dann komplett verdrängt und jetzt auch nicht drauf gekommen. Ist natürlich sonnenklar, wenn man es sieht.

Ja, Strahlensatz ;-)

Um die Frage "zu schwer" zu klären, wäre es interessant gewesen, die kongruente Unterteilung als Tipp zu posten.

Bei den beiden allgemeinen Fällen ist sie eher hinderlich.

Bis demnächst
Matthias

[Rolf b]

Um die Frage "zu schwer" zu klären, wäre es interessant gewesen, die kongruente Unterteilung als Tipp zu posten.

Bei den beiden allgemeinen Fällen ist sie eher hinderlich.

"Beide" allgemeine Fälle? Hab ich was übersehen in der Aufgabe? Für Gunnar war das doch der Schlüssel zur Lösung von Teilaufgabe b. Für Teilaufgabe a war's jedenfalls egal, da sieht man recht schnell dass das Konstrukt zu einem Rechteck wird und dann ist man mit Symmetrieüberlegungen schnell fertig.

Aber ob ich es mit dem Tipp geschafft hätte - keine Ahnung. Ich hatte ja sogar Probleme, BK=KP auf Anhieb zu sehen, bis mir κύριος Θαλῆς auf die Schulter tippte und φολλιδιοτ rief (und nein, ich kann kein Griechisch. Aber googeln).

Gruß
Rolf

[Matthias Apsel]

Hallo Rolf b,

Bei den beiden allgemeinen Fällen ist sie eher hinderlich.

"Beide" allgemeine Fälle? Hab ich was übersehen in der Aufgabe?

Ups. Verschrieben. Gemeint sind beide Fälle aus Aufgabe a)

Für Teilaufgabe a war's jedenfalls egal, da sieht man recht schnell dass das Konstrukt zu einem Rechteck wird und dann ist man mit Symmetrieüberlegungen schnell fertig.

Nur bei dem einfacheren der beiden Fälle. ;-)

Aber ob ich es mit dem Tipp geschafft hätte - keine Ahnung. Ich hatte ja sogar Probleme, BK=KP auf Anhieb zu sehen,

Gunnars Skizze allein ist schon genial. Das nicht Benötigte wegzulassen ist ungeheuer hilfreich.

Bis demnächst
Matthias

[Gunnar Bittersmann]

@@Rolf b

Ein Dreieck lässt sich durch die Seitenmittelpunkte in 4 kongruente Teildreiecke aufteilen. AHA! Vielleicht mal gewusst, aber wenn, dann komplett verdrängt und jetzt auch nicht drauf gekommen. Ist natürlich sonnenklar, wenn man es sieht.

Ja, das was der „Wie-man-leicht-sieht“-Teil in meinem Beweis. ;-)

Den Beweis dafür hab ich mir geschenkt; das sollte aber nicht allzu schwer sein.

Um die Frage "zu schwer" zu klären, wäre es interessant gewesen, die kongruente Unterteilung als Tipp zu posten.

Das wäre ja dann schon (fast) die Lösung der Aufgabe gewesen.

Wie ich unlängst bei einer anderen Aufgabe sagte, macht mitunter eine Hilfslinie den Unterschied zwischen einer schwierigen und einer leichten Aufgabe aus – und zwar bei dieser.

Wer findet sie?

LLAP 🖖

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Wie ich unlängst bei einer anderen Aufgabe sagte, macht mitunter eine Hilfslinie den Unterschied zwischen einer schwierigen und einer leichten Aufgabe aus – und zwar bei dieser.

Oder bei jener. Finde a.

Wer hier die Lösung nicht selbst sieht und sie dann präsentiert bekommt, dessen Kopf → Tisch.

LLAP 🖖

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Oder bei jener. Finde a.

Wer hier die Lösung nicht selbst sieht und sie dann präsentiert bekommt, dessen Kopf → Tisch.

Ich hab die Lösung in den Pen eingebaut. Über Change view in den Editor view gehen (oder im URI full durch pen ersetzen) und im Stylesheet für #solution das display: none rausnehmen.

Aber passt auf eure Tische auf!

LLAP 🖖

[Tabellenkalk]

Hallo,

Wer hier die Lösung nicht selbst sieht und sie dann präsentiert bekommt, dessen Kopf → Tisch.

Es ist zu offnsichtlich, dass a irgendwie von r abhängig ist. Baut man Nonsense-Info ein, z.b. rechte Winkel im Rechteck und eine Höhe des Rechtecks, sollte man das Kopf-Tisch-Geräusch vermutlich häufiger hören können.

Gruß
Kalk

[Matthias Apsel]

Hallo Gunnar Bittersmann,

Wie ich unlängst bei einer anderen Aufgabe sagte, macht mitunter eine Hilfslinie den Unterschied zwischen einer schwierigen und einer leichten Aufgabe aus – und zwar bei dieser.

Wer findet sie?

Ich weiß zwar nicht, welche Hilfslinie du meinst, aber ich habe das obere Dreieck an der Winkelhalbierenden gespiegelt. Fertig.

Bis demnächst
Matthias

[Rolf b]

Dann hast Du sie aber vorher neu - und richtig - gezeichnet. Oder?

[Gunnar Bittersmann]

@@Matthias Apsel

Ich weiß zwar nicht, welche Hilfslinie du meinst

Diese.

aber ich habe das obere Dreieck an der Winkelhalbierenden gespiegelt. Fertig.

Ich das untere. Schneller fertig. ;-)

LLAP 🖖

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Ich weiß zwar nicht, welche Hilfslinie du meinst

Diese.

aber ich habe das obere Dreieck an der Winkelhalbierenden gespiegelt. Fertig.

Ich das untere. Schneller fertig. ;-)

Wobei mein Gedankengang genau andersrum war: Ich hatte das gleichseitige Dreieck abgetrennt und dann gesehen, dass der verbleibende Teil die Spiegelung des unteren Dreiecks ist.

LLAP 🖖

[Rolf b]

Also bei der türkischen Aufgabe würde ich vermuten, dass bei ihrer Erstellung irgendwo ein schwarzes Loch in der Nähe war :) $$ x=7 $$

Für die Nummer mit dem Kreis brauche ich keine Linie, der sehe ich den trigonometrischen Pythagoras an :-)) Aber eine hilfreiche Linie sehe ich auch.

Rolf

[Rolf b]

Äh ja, autsch, natürlich $$ x=4 $$.

Meine Hilfslinie(n) bestand daraus, AD und BC zu verlängern. Schneidet sich in E. CE ist dann 4cm, ECD ist 60° und CDE auch, d.h. das angesetzte Dreieck ist gleichseitig mit Seitenlänge 4cm, das große Dreieck damit auch und x ist $$ 11cm-7cm=4cm $$.

Durch die vorsätzlich schiefe Zeichnung glaubt man dann nur seinem Ergebnis erstmal nicht. Bis man den Winkelmesser herausholt... :)

Ich frage mich nun, was die Herkunftsbezeichnung dieser Aufgabe ("from Turkey") mir sagen soll.
(a) die Türken haben kaputte Winkelmesser
(b) in der Türkei wird die Realität nur noch verzerrt wahrgenommen. Danke, Erdogan.
(c) die Aufgabe wurde von einem Truthahn gezeichnet

Rolf

[Matthias Apsel]

Hallo Rolf b,

Also bei der türkischen Aufgabe würde ich vermuten, dass bei ihrer Erstellung irgendwo ein schwarzes Loch in der Nähe war :) $$ x=7 $$

Leider falsch.

Bis demnächst
Matthias

[Rolf b]

Hab's ja schon vorher korrigiert :)

Allerdings bin ich wohl den Nachweis schuldig geblieben, dass $$\measuredangle EDC = 60^\circ$$ ist.

Die Winkel am Punkt D bezeichne ich von oben nach unten mit $$ \delta_1 (\measuredangle BDA)$$, $$\delta_2 (\measuredangle CDB)$$ und $$\delta_3 (\measuredangle EDC)$$.

Es ist

$$ 2\beta + 120^\circ + \delta_2+\delta_1+60^\circ = 360^\circ$$ (Winkelsumme Viereck)
$$ \Longleftrightarrow 2\beta + \delta_1 + \delta_2 = 180^\circ $$

Damit ist $$2\beta = \delta_3$$, weil ja $$\delta_1 + \delta_2 + \delta_3$$ einen gestreckten Winkel bilden. $$\bigtriangleup$$ CED und $$\bigtriangleup$$ BEA haben demnach 3 gleiche Winkel, nur mit unterschiedlicher Umlaufrichtung. D.h. das eine ist zur Spiegelung des anderen ähnlich, also demnach mindestens mal gleichschenklig. Und ein gleichschenkliges Dreieck, wo ein Winkel $$60^\circ$$ beträgt, ist gleichseitig. Es folgt $$\measuredangle EDC = 60^\circ$$, q.e.d :)

Gruß
Rolf

[Gunnar Bittersmann]

@@Rolf b

Für die Nummer mit dem Kreis brauche ich keine Linie, der sehe ich den trigonometrischen Pythagoras an :-))

Wenn du den Pythagoras siehst, brauchst du doch eine Linie.

LLAP 🖖

[Rolf b]

Nein. Ich sehe die Horizontale x und die Vertikale y. Sie bilden zusammen mit a ein rechtwinkliges Dreieck. Also ist $$a^2 = x^2+y^2$$. Nun bilden aber x und y den cosinus und sinus des Winkels zu dem Punkt, wo das Rechteck den Kreis berührt. Diesen Winkel habe ich tatsächlich gesehen, ohne mir Gedanken darüber zu machen, dass der entsprechende Winkelschenkel eine Diagonale des Rechtecks ist und Länge r hat. Es ist also $$x=r\cdot sin\alpha$$ und $$y=r\cdot cos\alpha$$, r klammert sich aus, $$sin^2\alpha+cos^2\alpha$$ ist bekanntlich gleich 1 und darum ist $$a^2=r^2$$ und $$a=\pm r$$.

Das ist jetzt nichts, worauf ich stolz sein kann. Es zeigt nur, wie schwer ich mich damit tue, Dinge geometrisch zu sehen. Ich stürze mich immer gleich auf algebraische Überlegungen...

Rolf

[Gunnar Bittersmann]

@@Rolf b

Nein. Ich sehe die Horizontale x und die Vertikale y. Sie bilden zusammen mit a ein rechtwinkliges Dreieck. Also ist $$a^2 = x^2+y^2$$.

Richtig. Aber irrelevant.

Nun bilden aber x und y den cosinus und sinus des Winkels zu dem Punkt, wo das Rechteck den Kreis berührt.

Richtig. Aber irrelevant.

Diesen Winkel habe ich tatsächlich gesehen, ohne mir Gedanken darüber zu machen, dass der entsprechende Winkelschenkel eine Diagonale des Rechtecks ist und Länge r hat.

Punkt.

Es ist also $$x=r\cdot sin\alpha$$ und $$y=r\cdot cos\alpha$$, r klammert sich aus, $$sin^2\alpha+cos^2\alpha$$ ist bekanntlich gleich 1 und darum ist $$a^2=r^2$$ und $$a=\pm r$$.

Was soll das denn noch?

Das ist jetzt nichts, worauf ich stolz sein kann. Es zeigt nur, wie schwer ich mich damit tue, Dinge geometrisch zu sehen. Ich stürze mich immer gleich auf algebraische Überlegungen...

Da hab ich noch eine schöne Aufgabe parat, wo man genau das nicht tun soll. Die ist dann allerdings auch etwas schwerer. Mathematik zum Monatsende?

LLAP 🖖

[Rolf b]

Hallo Gunnar,

ob irrelevant oder nicht, so sind meine Gedanken nun mal verlaufen. Wenn man deine fette rote Diagonale nicht vor Augen hat, sondern nur die andere, und das rechtwinklige Dreieck, die sie mit x und y bildet, mit dem rechten Winkel am Kreisbogen, dann erschließt sich die Länge von a auf diese Weise.

Rolf

[Gunnar Bittersmann]

@@Rolf b

Es ist also $$x=r\cdot sin\alpha$$ und $$y=r\cdot cos\alpha$$

BTW, kursiv werden Bezeichner von Variablen, Punkten etc. gesetzt, nicht aber Bezeichner von Opearatoren (Funktionen) wie Winkel- und Logarithmusfunktionen, lim, sgn, min, max, d (Differential).

Für etliche Funktionsbezeichner gibt es in TeX spezielle Schreibweisen: \sin, \cos, siehe Funktionsbezeichnungen.

x=r\cdot \sin\alpha ergibt $$x=r\cdot \sin\alpha$$

Und wie ich Matthias in diesem Thread schon zu bedenken gab, hat man bei LaTeX hier im Forum immer einen unschönen FOUT: erst wird der Quelltext angezeigt, dann mit spürbarer Verzögerung die gerenderte Formel.

Bei einfachen Formeln kann (sollte?) man auf LaTeX verzichten und Markdown und Unicode-Zeichen verwenden:

_x_ = _r_ · sin _α_ ergibt x = r · sin α

LLAP 🖖

[Gunnar Bittersmann]

@@Rolf b

Es ist also $$x=r\cdot sin\alpha$$ und $$y=r\cdot cos\alpha$$

Da das hier nicht relevant war, hatte ich da nicht genauer hingesehen (von den kursiv gesetzten Funktionsbezeichnern mal abgesehen).

Mir scheint, du hättest Sinus und Cosinus verwechselt (oder halt x und y).

LLAP 🖖

[Rolf b]

Dir scheint die Sonne aus den Fingern. Hast natürlich recht.

[Der-Dennis]

Hallo Matthias,

Ist ja rege Beteiligung hier.

Ja. Leider. Woran lags?

bei mir einfach nur an akutem Zeitmangel. Hab jetzt aber alle Mathe- und Physikrätsel (was wohl als nächstes kommt?) nachgeholt. Nur das Rätsel von @Gunnar Bittersmann hebe ich mir für nen kalten Winterabend auf, so wie sich das anhört :-) Alles tolle Rätsel, danke dafür.

Gruß
Dennis

[Matthias Apsel]

Hallo Der-Dennis,

(was wohl als nächstes kommt?) nachgeholt.

CSS. Und ich habe keine Lösung dafür.

Nur das Rätsel von @Gunnar Bittersmann hebe ich mir für nen kalten Winterabend auf, so wie sich das anhört :-)

eher für eine Polarnacht ;-)

Alles tolle Rätsel, danke dafür.

Bitte. Gern.

Bis demnächst
Matthias

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Ist ja rege Beteiligung hier.

Oh, es ist Leben in den Thread gekommen. Aber passt jemand auf? Nein!

Damit gilt auch KP = ML und MK = LQ.

So weit, so gut.

Damit sind die Dreiecke MPK und MLQ kongruent

Und wenn der Topf Winkel ∠_BCA_ aber nun ein rechter ist? Dann liegen M, K und P auf einer Linie, ebenso M, L, und Q; es gibt also gar keine Dreiecke MPK und MLQ.

Von entarteten Dreiecken mit φ = ψ = 0 zu sprechen ist wohl nicht ganz sauber. Machen wir lieber eine Fallunterscheidung:

Nun ist ∠_PMQ_ ≡ ∠_KML_ = ∠_BCA_= 1∟, das Dreieck MPQ ist somit rechtwinklig.

MP = MK + KP = LQ + ML = MQ. Das Dreieck MPQ ist somit gleichschenklig.

LLAP 🖖

[Matthias Apsel]

Hallo Gunnar Bittersmann,

Hier trotzdem noch die Skizzen für die beiden einfachen Varianten:

1. Fall: Die Dreiecke werden über den Katheten errichtet

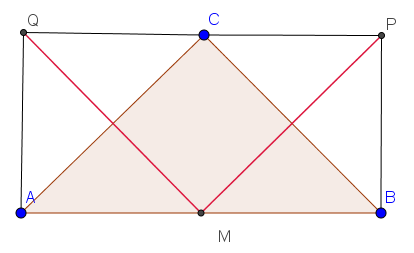
Die Dreiecke ABC und MPQ sind kongruent.

2. Fall: Die Dreiecke werden über der Hypothenuse und einer Kathete errichtet

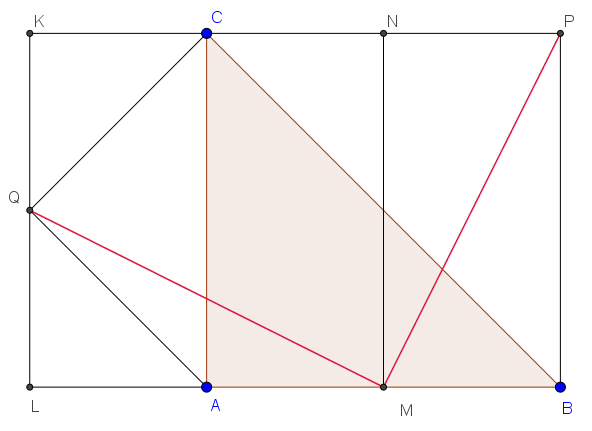
• die Quadrate ABPC und LMNK sind kongruent
• die Strecken MQ und MP verlaufen vom Mittelpunkt einer Quadratseite zu einem gegenüberliegenden Eckpunkt sind also gleichlang
• die Winkel ∠LMQ und ∠PMB betragen zusammen 90°
• deshalb ist der Winkel ∠PMQ auch 90°

Bis demnächst
Matthias