nicht angemeldet
Mathematik zum Wochenende
Matthias Apsel
Mathematik zum Wochenende
Matthias Apsel
Camping_RIDER
Gunnar BittersmannHallo alle,
Das Liebespaar Paul und Paula verabredet sich. Sie vereinbaren folgendes:
Sie treffen sich zwischen 21 und 22 Uhr auf der Liebesinsel. Da sie aber nicht wissen, ob und wie lange ihre Eltern aufpassen, können sie keinen konkreten Zeitpunkt benennen. Sie werden also zu einem zufälligen Zeitpunkt dort ankommen und falls der Partner nicht da ist entweder nach 15 Minuten oder um 22:00 Uhr den Treffpunkt verlassen, je nach dem, was eher eintritt.
Wie groß ist die Wahrscheinlichkeit, dass sich die Beiden treffen?
Bis demnächst
Matthias
--
Rosen sind rot.
Rosen sind rot.
-
Hallo
Ich gehe davon aus, dass beide innerhalb der vorgegebenen Stunde auch dort erscheinen.
Dann nehme ich die 25%.
Gruss
MrMurphy
-
Aloha ;)
Ich gehe davon aus, dass beide innerhalb der vorgegebenen Stunde auch dort erscheinen.
Davon gehe ich auch aus.
Dann nehme ich die 25%.
Ich komme nur auf etwa 22%, kann mich aber auch vertan haben. Ist etwas tricky, mit den Minuten zu jonglieren.
Grüße,
RIDER
-
@@Camping_RIDER
Ich komme nur auf etwa 22%, kann mich aber auch vertan haben. Ist etwas tricky, mit den Minuten zu jonglieren.
Ich komme auf etwa das Doppelte. Der Trick ist, nicht mit Minuten zu jonglieren. ;-)
LLAP 🖖
--
“When UX doesn’t consider all users, shouldn’t it be known as ‘Some User Experience’ or... SUX? #a11y” —Billy Gregory-
Aloha ;)
Ich komme nur auf etwa 22%, kann mich aber auch vertan haben. Ist etwas tricky, mit den Minuten zu jonglieren.
Ich komme auf etwa das Doppelte. Der Trick ist, nicht mit Minuten zu jonglieren. ;-)
Da gehe ich von aus, bin nur mal gespannt, ob das mit dem Minuten-jonglieren nicht auch funktioniert. Sollte eigentlich.
Matthias hat mir verraten, dass das Ergebnis falsch ist, aber den Fehler im Rechenweg oder den logischen Stolperstein unterwegs habe ich bislang nicht gefunden.
Grüße,
RIDER
-
Hallo Gunnar Bittersmann,
Ich komme auf etwa das Doppelte.
Und zwar ziemlich genau: Die Differenz zwischen deiner Lösung und dem Doppelten von Riders Lösung beträgt $$\tfrac{1}{240}$$.
Bis demnächst
Matthias--
Rosen sind rot.-
Aloha ;)
Ich komme auf etwa das Doppelte.
Und zwar ziemlich genau: Die Differenz zwischen deiner Lösung und dem Doppelten von Riders Lösung beträgt $$\tfrac{1}{240}$$.
Tatsächlich? Weil Gunnar um $$\tfrac{1}{240}$$ daneben liegt und ich vergessen habe zu verdoppeln, weil mein o.B.d.A.-Gedanke doch Müll war? 😂
Oder nur zufällig?
Grüße,
RIDER
-
Hallo Camping_RIDER,
Tatsächlich?
Tatsächlich.
Weil Gunnar um $$\tfrac{1}{240}$$ daneben liegt und ich vergessen habe zu verdoppeln, weil mein o.B.d.A.-Gedanke doch Müll war? 😂
Meiner Meinung nach ist dein o.B.d.A.-Gedanke falsch, ja.
Aber du liegst um $$\tfrac{1}{240}$$ daneben.
Bis demnächst
Matthias--
Rosen sind rot.-
Aloha ;)
Meiner Meinung nach ist dein o.B.d.A.-Gedanke falsch, ja.
Ja, geschenkt.
Aber du liegst um $$\tfrac{1}{240}$$ daneben.
Das war etwa was ich mit dem problematischen jonglieren meinte.
Das ist entweder eine doppelt eingerechnete Minute (dann die 45.) oder eine zu wenig eingerechnete (dann die 60. bzw. die 1.).
Sags mir nicht, das krieg ich selber noch raus.
Grüße,
RIDER
-
Aloha ;)
Aber du liegst um $$\tfrac{1}{240}$$ daneben.
Das war etwa was ich mit dem problematischen jonglieren meinte.
Das ist entweder eine doppelt eingerechnete Minute (dann die 45.) oder eine zu wenig eingerechnete (dann die 60. bzw. die 1.).
Sags mir nicht, das krieg ich selber noch raus.
Mein Urteil lautet: Beim Verdoppeln wird in meinem alten Lösungsweg eine Treffwahrscheinlichkeit mit verdoppelt, die nur einmal vorkommt (namentlich die Wahrscheinlichkeit, in den letzten 15 Minuten in der selben Minute einzutreffen - bei den ersten 45 Minuten ist das irrelevant, weil dort nicht mit diskreten Minuten gerechnet wurde). Demnach ist das Doppelte meiner Lösung um $$\tfrac{1}{240}$$ zu hoch, da das genau die Größe dieser Treffwahrscheinlichkeit darstellt.
Grüße,
RIDER
-
-
-
Aloha ;)
Weil [...] ich vergessen habe zu verdoppeln, weil mein o.B.d.A.-Gedanke doch Müll war
Ich hätte wohl nicht zu o.B.d.A. greifen sollen, sondern zu einer Fallunterscheidung, in der der zweite Fall analog zum ersten ist. Tja. Doof gelaufen. xD
Grüße,
RIDER
-
-
-
-
-
Hey,
Ich gehe davon aus, dass beide innerhalb der vorgegebenen Stunde auch dort erscheinen.
Laut meiner Rechnung kommt Sie nach 22 Uhr, könnte mich aber auch verrechnet haben.
Gruß
Jo-
Aloha ;)
Laut meiner Rechnung kommt Sie nach 22 Uhr, könnte mich aber auch verrechnet haben.
Wenn sich die beiden zwischen 21 und 22 Uhr treffen kommt sie sicher erst nach 22 ... oh wait, ich glaube ich habe dich eben falsch verstanden.
Grüße,
RIDER
-
-
-
Hallo Matthias Apsel,
Für die, die es schon raus haben oder nah dran sind: Wie ist die Wartezeit zu wählen, damit die Wahrscheinlichkeit eines Treffens 0,75 beträgt?
Bis demnächst
Matthias--
Rosen sind rot.-
Hallo
45 Minuten.
Gruss
MrMurphy
-
Aloha ;)
Für die, die es schon raus haben oder nah dran sind: Wie ist die Wartezeit zu wählen, damit die Wahrscheinlichkeit eines Treffens 0,75 beträgt?
Meine korrigierte und verallgemeinerte Formel sagt exakt 30 Minuten.
Grüße,
RIDER
-
@@Camping_RIDER
Meine korrigierte und verallgemeinerte Formel sagt exakt 30 Minuten.
Da komme ich durch die Überlegung, die mich bei 15 Minuten Wartezeit zu etwa 44% Prozent führte, auch drauf.
LLAP 🖖
--
“When UX doesn’t consider all users, shouldn’t it be known as ‘Some User Experience’ or... SUX? #a11y” —Billy Gregory -
Ja, für die Wahrscheinlichkeit 0,75 sind es 30 Minuten. Noch ein paar Wertepaare:
18 Min -> 0,51
24 Min -> 0,64
30 Min -> 0,75
36 Min -> 0,84
Stimmts?
-
-
-
-
Hier steht ein Lösungsversuch
Nicht lesen, wer selber weiter rätseln will
erreichbar über den Link (Versionen) im Kopf des Beitrages.
Edit: Was ist eigentlich das sinnvollste Vorgehen mit einer Lösung? Dem Threadersteller schicken? Mit Spoileralarm versehen und hier reinstellen?
-
Hallo encoder,
Hier steht ein Lösungsversuch
Nicht lesen, wer selber weiter rätseln will
Du kannst die Ideen auch gern per PM verschicken.
Bis demnächst
Matthias--
Rosen sind rot.
-
-
Hallo alle,
Wir nennen unser Liebespaar nun Xaver und Yvonne, damit die Achsenbezeichnung so bleiben kann. Wir tragen die möglichen Paare von Ankunftszeiten in ein Koordinatensystem ein.
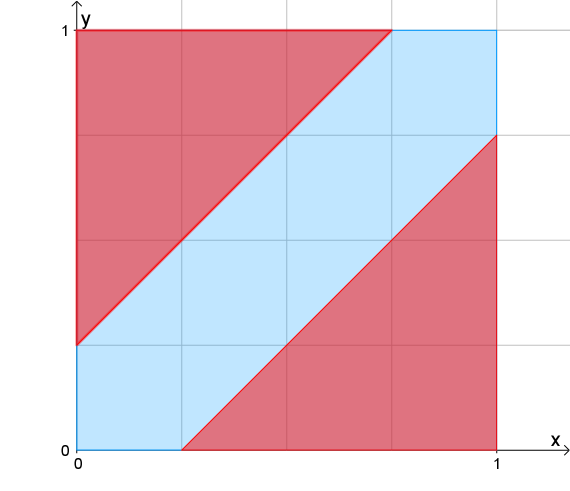
Der blaue Abschnitt auf der x-Achse ist Xavers Wartezeit, der blaue Abschnitt auf der y-Achse ist Yvonnes Wartezeit. Es ist offensichtlich, dass die beiden sich im blauen Korridor treffen und sonst verfehlen.
Der Gesamtflächeninhalt beträgt 1 (h²), die beiden roten Flächen bilden ein Quadrat der Seitenlänge $$\tfrac{3}{4}$$, ergibt als Flächeninhalt $$\tfrac{9}{16}$$. Mithin ist die blaue Fläche $$1- \tfrac{9}{16} = \tfrac{7}{16}$$ groß, das ist die gesuchte Wahrscheinlichkeit.
Wenn die Treffenswahrscheinlichkeit 75% – also $$\tfrac{3}{4}$$ – betragen soll, muss die rote Fläche $$\tfrac{1}{4}$$ sein, das ist für eine Seitenlänge von $$\tfrac{1}{2}$$ der Fall, was 30 Minuten Wartezeit bedeutet.
Die Formel für die Wahrscheinlichkeit eines Treffens in Abhängigkeit von der Wartezeit in Stunden lautet: $$p(w) = 1 - (1-w)^{2} = - w^{2}+ 2w$$. Das bedeutet auch, dass die Wahrscheinlichkeit, dass beide zum exakt gleichen Zeitpunkt aufschlagen, null ist.
Bis demnächst
Matthias--
Rosen sind rot.-
Aloha ;)
Sehr schön erklärt - Danke für den Input!
Die Formel für die Wahrscheinlichkeit eines Treffens in Abhängigkeit von der Wartezeit in Stunden lautet: $$p(w) = 1 - (1-w)^{2} = - w^{2}+ 2w$$. Das bedeutet auch, dass die Wahrscheinlichkeit, dass beide zum exakt gleichen Zeitpunkt aufschlagen, null ist.
Die letzte Aussage halte ich allerdings für inhaltlich falsch (oder zumindest fehlinterpretiert)! Es ist vielmehr so, dass das gesamte Modell und damit auch die Formel nur für Wartezeiten $$w \in (0,60]$$ definiert ist; bei einer Wartezeit von Null ist ein Treffen nicht mehr möglich, aber genausowenig eine Aussage über Ankunftszeiten.
Inhaltlich gesehen ist ein (unmöglicher) Erfolg bei einer Wartezeit von null nicht das selbe, wie, dass beide zum gleichen Zeitpunkt aufschlagen; immerhin ist auch bei einer Wartezeit > Null noch ein exakt gleichzeitiges Eintreffen möglich. Die Frage nach der Gleichzeitigkeit des Eintreffens ist demnach also unabhängig von der Wartezeit zu betrachten!
Was stimmt ist, ganz unabhängig von der errechneten Formel und auch ganz unabhängig von der Wartezeit, dass die Wahrscheinlichkeit, exakt gleichzeitig einzutreffen ohne dabei ein Toleranzzeitfenster zuzugestehen, grundsätzlich gegen Null strebt - aber eben immer noch größer Null ist.
Grüße,
RIDER
-
Hallo Camping_RIDER,
Sehr schön erklärt - Danke für den Input!
Gern.
Das bedeutet auch, dass die Wahrscheinlichkeit, dass beide zum exakt gleichen Zeitpunkt aufschlagen, null ist.
Die letzte Aussage halte ich allerdings für inhaltlich falsch (oder zumindest fehlinterpretiert)!
Inhaltlich falsch, ja. Weil die Modellierung Grenzen hat. Die Gleichung stimmt für eine stetige Zufallsgröße.
Was stimmt ist, ganz unabhängig von der errechneten Formel und auch ganz unabhängig von der Wartezeit, dass die Wahrscheinlichkeit, exakt gleichzeitig einzutreffen ohne dabei ein Toleranzzeitfenster zuzugestehen, grundsätzlich gegen Null strebt - aber eben immer noch größer Null ist.
Nur bei diskreten Zufallsgrößen.
Bis demnächst
Matthias--
Rosen sind rot.
-
-
Wenn ich nicht wieder mal falsch im Kopfrechnen gewesen wäre, hätte ich das mit meiner Überlegung auch heraus bekommen :-)
Die grafische Darstellung bzw. Erklärung finde ich klasse! -
Hallo Matthias,
sehr elegante Lösung! (Und sie kommt ohne die nicht angemessene Diskretisierung der Zeit aus.)
Ich war auf die gleiche Formel P(w) = 2w - w² gekommen, indem ich die Wahrscheinlichkeitsdichte p(t) als Funktion des Zeitpunkts t des Eintreffens von Paul (im Intervall [0;1], als Bruchteil der Stunde) aufgetragen habe.
Mit der Wartezeit w (dito) hat p(t) für den Fall, dass t genügend weit von 0 bzw 1 entfernt ist, den Wert 2w (denn das Zeitfenster, das Paula erwischen muss, ist der Bruchteil 2w von einer Stunde).
Ist t kleiner als w oder größer als 1-w, wird das Zeitfenster beschnitten, und zwar in linearer Weise bis zum kleinsten Wert w. So ergibt sich der gezeichnete Graph der Wahrscheinlichkeitsdichte (rot).
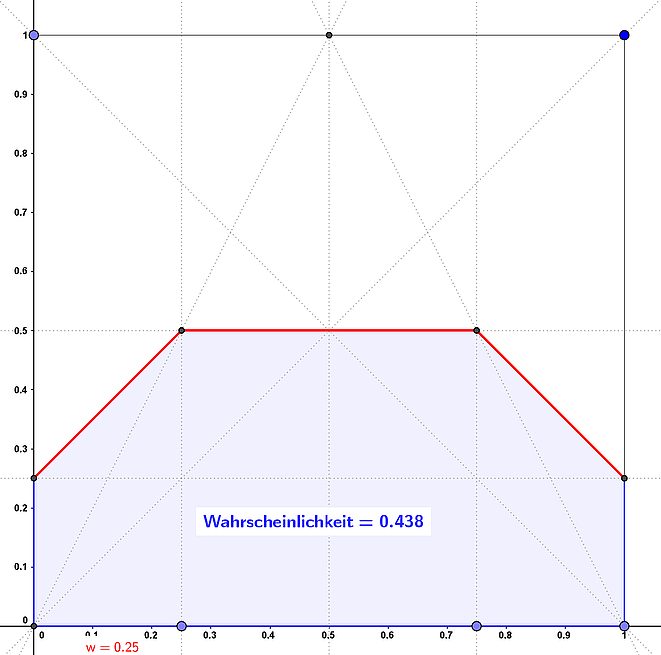
Die gesuchte Wahrscheinlichkeit, dass Paula auf Paul trifft, erhält man dann als Flächenwert unter dem Graphen, also als Differenz aus dem Rechteck mit Breite 1 und Höhe 2w und den beiden halben Quadraten der Kantenlänge w - also die obige Formel. (Für w > 0.5 wird die Flächenberechnung etwas umständlicher, hat aber das selbe Ergebnis.)
Das war eine nette Aufgabe.
-
Aloha ;)
sehr elegante Lösung! (Und sie kommt ohne die nicht angemessene Diskretisierung der Zeit aus.)
Ich habe die Zeit teilweise diskretisiert. Hier mal noch meine Lösung (die umständlichste von Allen, nehme ich an).
Sei die Wahrscheinlichkeit, zu einer bestimmten Minute einzutreffen, für beide Partner über die gesamte Stunde hinweg gleichverteilt.
Fall 1 - Paula trifft in den ersten 45 Minuten zuerst oder zeitgleich ein
Paula trifft mit einer Wahrscheinlichkeit von $$\frac{45}{60} = \frac{3}{4}$$ innerhalb der ersten 45 Minuten (also zwischen 21:00:00 und 21:44:59) ein. Sie wartet dann jeweils 15 Minuten auf ihren Liebsten und geht dann wieder. Die Wahrscheinlichkeit, dass Paul innerhalb von irgendwelchen 15 Minuten eintrifft, ist $$\frac{15}{60} = \frac{1}{4}$$ und damit ist die Wahrscheinlichkeit, dass sich Paula und Paul treffen genau $$\frac{3}{4} \cdot \frac{1}{4} = \frac{3}{16} = \frac{45}{240}$$, falls Paula vor 21:45 erscheint.
Fall 2 - Paula trifft in den letzten 15 Minuten zuerst ein
Bleibt noch zu betrachten was passiert, wenn Paula nach 21:45 (also zwischen 21:45:00 und 21:59:59) erscheint. Sei $$x \in [1,15]$$ die Anzahl der Minuten, die nach 21:45 bis zu Paulas Eintreffen noch begonnen haben. Dann hat Paul noch $$15-x$$ Minuten mit der Möglichkeit, zu erscheinen (wenn wir annehmen, dass Paul frühestens in der Minute nach Paulas Eintreffen erscheint). Wir bekommen damit dann folgende Wahrscheinlichkeit, dass sich Paula und Paul treffen, wenn Paula nach 21:45 als erste erscheint:
$$ \frac{1}{60} \cdot \sum_{i = 1}^{15} \frac{15-x}{60} = \frac{1}{60 \cdot 60} \cdot \left( 15 \cdot 15 - \sum_{x = 1}^{15} x \right) = \frac{1}{3600} \cdot \left( 15 \cdot 15 - \frac{15 \cdot 16}{2} \right) = \frac{105}{3600} = \frac{7}{240}$$
Fall 3 - Paul trifft in den ersten 45 Minuten zuerst oder zeitgleich ein
Die Überlegungen sind hier exakt analog zu Fall 1, also ergibt sich auch hier eine Aufeinandertreff-Wahrscheinlichkeit von $$\frac{45}{240}$$
Fall 4 - Paul trifft in den letzten 15 Minuten zuerst ein
Die Überlegungen sind hier exakt analog zu Fall 2, also ergibt sich auch hier eine Aufeinandertreff-Wahrscheinlichkeit von $$\frac{7}{240}$$
Fall 5 - Beide treffen innerhalb der letzten 15 Minuten in der selben Minute ein
Die Wahrscheinlichkeit, dass beide innerhalb einer Minute eintreffen, ist $$\frac{1}{60} \cdot \frac{1}{60}$$, also über 15 Minuten $$\frac{15}{3600} = \frac{1}{240}$$
Demnach liegt die Wahrscheinlichkeit, dass beide sich treffen, bei $$ 2 \cdot \frac{45}{240}+ 2 \cdot \frac{7}{240} + \frac{1}{240} = \frac{105}{240} = \frac{7}{16} \approx 44 % $$
bzw. verallgemeinert:
Fall 1 - Paula trifft in den ersten 60-w Minuten zuerst oder zeitgleich ein
Paula trifft mit einer Wahrscheinlichkeit von $$\frac{60-w}{60}$$ innerhalb der ersten $$60-w$$ Minuten ein. Sie wartet dann jeweils w Minuten auf ihren Liebsten und geht dann wieder. Die Wahrscheinlichkeit, dass Paul innerhalb von irgendwelchen w Minuten eintrifft, ist $$\frac{w}{60}$$ und damit ist die Wahrscheinlichkeit, dass sich Paula und Paul treffen genau $$\frac{60-w}{60} \cdot \frac{w}{60} = \frac{60w-w^2}{3600}$$, falls Paula spätestens w Minuten vor 22 Uhr erscheint.
Fall 2 - Paula trifft in den letzten w Minuten zuerst ein
Bleibt noch zu betrachten was passiert, wenn Paula in den letzten w Minuten erscheint. Sei $$x \in [1,w]$$ die Anzahl der Minuten, die zwischen w Minuten vor 22 Uhr und bis zu Paulas Eintreffen noch begonnen haben. Dann hat Paul noch $$w-x$$ Minuten mit der Möglichkeit, zu erscheinen (wenn wir annehmen, dass Paul frühestens in der Minute nach Paulas Eintreffen erscheint). Wir bekommen damit dann folgende Wahrscheinlichkeit, dass sich Paula und Paul treffen, wenn Paula frühestens w Minuten vor 22 Uhr als erste erscheint:
$$ \frac{1}{60} \cdot \sum_{x = 1}^{w} \frac{w-x}{60} = \frac{1}{60 \cdot 60} \cdot \left( w^2 - \sum_{x = 1}^{w} x \right) = \frac{1}{3600} \cdot \left( w^2 - \frac{w \cdot (w+1)}{2} \right) = \frac{w^2-w}{7200}$$
Fall 3 - Paul trifft in den ersten 60-w Minuten zuerst oder zeitgleich ein
Analog zu Fall 1.
Fall 4 - Paul trifft in den letzten w Minuten zuerst ein
Analog zu Fall 2.
Fall 5 - Beide treffen innerhalb der letzten w Minuten in der selben Minute ein
Die Wahrscheinlichkeit, dass beide innerhalb einer Minute eintreffen, ist $$\frac{1}{60} \cdot \frac{1}{60}$$, also über w Minuten $$\frac{w}{3600}$$
Demnach liegt die Wahrscheinlichkeit, dass beide sich treffen, bei $$ P = 2 \cdot \frac{60w-w^2}{3600}+ 2 \cdot \frac{w^2-w}{7200} + \frac{w}{3600} = \frac{120w-w^2}{3600} $$
Betrachte jetzt $$P \geq 75%$$:
$$\frac{120w-w^2}{3600} \geq 75%$$
$$120w-w^2 \geq 2700$$
$$ 30 \leq w \leq 90$$
Damit muss die Wartezeit für eine 75%ige Antreffwahrscheinlichkeit mindestens 30 Minuten betragen.
Das zeigt jetzt mal wieder, dass es verdammt viele Wege gibt, ans Ziel zu kommen. Nur sind leider nicht alle davon sinnvoll oder geschickt 😂
Grüße,
RIDER
P.S.: Das fanden meine Prüfer übrigens heute auch. Bestanden hab ich trotzdem - gerade so. Aber immerhin bin ich jetzt auch staatsexaminierter Mathematiker 😂
-
Hallo Camping_RIDER,
P.S.: Das fanden meine Prüfer übrigens heute auch. Bestanden hab ich trotzdem - gerade so. Aber immerhin bin ich jetzt auch staatsexaminierter Mathematiker 😂
Glückwunsch! 🌹
Bis demnächst
Matthias--
Rosen sind rot.-
Aloha ;)
P.S.: Das fanden meine Prüfer übrigens heute auch. Bestanden hab ich trotzdem - gerade so. Aber immerhin bin ich jetzt auch staatsexaminierter Mathematiker 😂
Glückwunsch! 🌹
Danke 😂
Grüße,
RIDER
-
-
-
-