Mathematik zum Wochenende - Auflösung

[Matthias Apsel]

Hallo alle,

Wir nennen unser Liebespaar nun Xaver und Yvonne, damit die Achsenbezeichnung so bleiben kann. Wir tragen die möglichen Paare von Ankunftszeiten in ein Koordinatensystem ein.

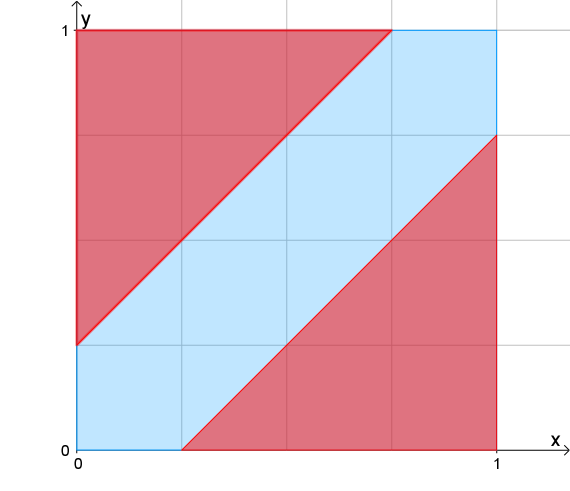
Der blaue Abschnitt auf der x-Achse ist Xavers Wartezeit, der blaue Abschnitt auf der y-Achse ist Yvonnes Wartezeit. Es ist offensichtlich, dass die beiden sich im blauen Korridor treffen und sonst verfehlen.

Der Gesamtflächeninhalt beträgt 1 (h²), die beiden roten Flächen bilden ein Quadrat der Seitenlänge $$\tfrac{3}{4}$$, ergibt als Flächeninhalt $$\tfrac{9}{16}$$. Mithin ist die blaue Fläche $$1- \tfrac{9}{16} = \tfrac{7}{16}$$ groß, das ist die gesuchte Wahrscheinlichkeit.

Wenn die Treffenswahrscheinlichkeit 75% – also $$\tfrac{3}{4}$$ – betragen soll, muss die rote Fläche $$\tfrac{1}{4}$$ sein, das ist für eine Seitenlänge von $$\tfrac{1}{2}$$ der Fall, was 30 Minuten Wartezeit bedeutet.

Die Formel für die Wahrscheinlichkeit eines Treffens in Abhängigkeit von der Wartezeit in Stunden lautet: $$p(w) = 1 - (1-w)^{2} = - w^{2}+ 2w$$. Das bedeutet auch, dass die Wahrscheinlichkeit, dass beide zum exakt gleichen Zeitpunkt aufschlagen, null ist.

Bis demnächst
Matthias