nicht angemeldet
Hallo Matthias,
sehr elegante Lösung! (Und sie kommt ohne die nicht angemessene Diskretisierung der Zeit aus.)
Ich war auf die gleiche Formel P(w) = 2w - w² gekommen, indem ich die Wahrscheinlichkeitsdichte p(t) als Funktion des Zeitpunkts t des Eintreffens von Paul (im Intervall [0;1], als Bruchteil der Stunde) aufgetragen habe.
Mit der Wartezeit w (dito) hat p(t) für den Fall, dass t genügend weit von 0 bzw 1 entfernt ist, den Wert 2w (denn das Zeitfenster, das Paula erwischen muss, ist der Bruchteil 2w von einer Stunde).
Ist t kleiner als w oder größer als 1-w, wird das Zeitfenster beschnitten, und zwar in linearer Weise bis zum kleinsten Wert w. So ergibt sich der gezeichnete Graph der Wahrscheinlichkeitsdichte (rot).
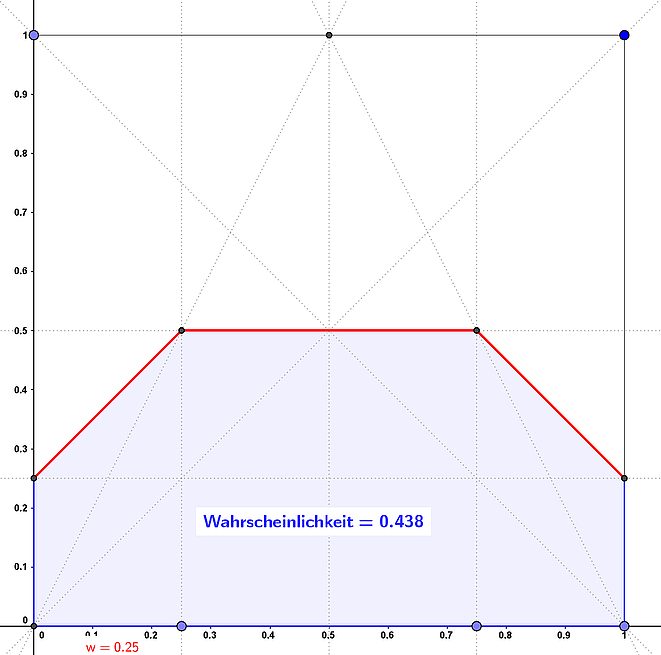
Die gesuchte Wahrscheinlichkeit, dass Paula auf Paul trifft, erhält man dann als Flächenwert unter dem Graphen, also als Differenz aus dem Rechteck mit Breite 1 und Höhe 2w und den beiden halben Quadraten der Kantenlänge w - also die obige Formel. (Für w > 0.5 wird die Flächenberechnung etwas umständlicher, hat aber das selbe Ergebnis.)
Das war eine nette Aufgabe.
Matthias Apsel
Camping_RIDER
Gunnar Bittersmann