Mathematik zum langen Wochenende - Lösung

[Matthias Apsel]

Hallo alle,

so, mal eine erste Lösung:

Es gab übrigens wie immer mehrere Lösungswege, vielleicht veröffentlichen ja die Autoren ihre auch.

Ich nehme eine Strecke der Länge 1 und lege auf ihr zwei Stellen x und y fest. Ohne Beschränkung der Allgemeinheit sei x < y. Die gekennzeichnete Punktmenge erfüllt diese Bedingungen.

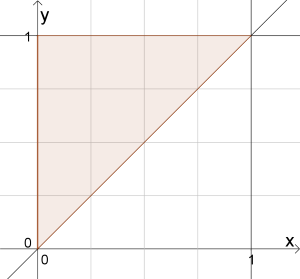
Die Dreiecksseiten sind dann: x, y-x und 1-y. Jede dieser Seiten darf höchstens 1/2 sein. Daraus folgt

• x < 1/2
• y > 1/2
• y-x < 1/2 ⇒ y < x + 1/2

Anmerkung:

Wer das mit dem 1/2 nicht sieht oder glaubt, da es ja nur eine obere Schranke für die Dreiecksungleichung ist, der kann auch drei mal die Dreiecksungleichung anwenden.

• x < y-x + 1-y
• y-x < x + 1-y
• 1-y < x + y-x

Durch Umformung ergeben sich die obigen 3 Ungleichungen.

Die blau gekennzeichnete Punktmenge erfüllt alle Bedingungen.

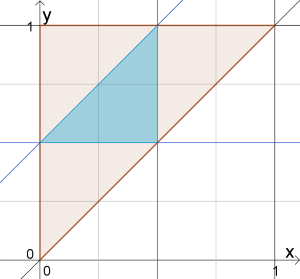
Das Verhältnis von blauer zu roter Fläche ist 1/4.

Bis demnächst
Matthias