@@Gunnar Bittersmann
Ich stelle mal meine Lösung vor (die sich im Wesentlichen mit Camping_RIDERs deckt und auch mit der, die mir Rolf b per DM zukommen ließ):
Wie wir bereits gesehen haben, reichen 3 Runden gerade so aus, um alle Seitenflächen der 1er-Würfel zu bemalen. Keine Fläche darf übermalt werden.
Um am Ende zweifarbig zu sein, muss ein 1er-Würfel einmal im Zentrum des 3er-Würfels gewesen sein. Ein 1er-Würfel darf höchstens einmal im Zentrum sein; d.h. in jeder Runde muss ein anderer 1er-Würfel im Zentrum sein. Da es 3 Runden gibt, gibt es am Ende 3 zweifarbige Würfel – wenn denn die Bemalung überhaupt möglich ist.
Und so geht’s: Wir betrachten 3 Zeitpunkte (in den 3 Runden), wo die 1er-Würfel zum 3er-Würfel zusammengesetzt sind und der Maler jeweils seine Arbeit getan hat. (Wie hieß der Mann der Frau des Malers? Aber das ist ein anderes Rätsel.)
Ein 1er-Würfel kann in 4 verschiedenen Zuständen (Positionen im 3er-Würfel) sein:
- Z — im Zentrum; keine Fläche frisch gestrichen
- F – in einem Flächenmittelpunkt; 1 Fläche frisch gestrichen
- K – in einem Kantenmittelpunkt; 2 Flächen frisch gestrichen
- E – in einer Ecke; 3 Flächen frisch gestrichen
Es ist zu jedem der 3 Zeitpunkte jeweils 1 Würfel im Zustand Z, 6 im Zustand F, 12 im Zustand K und 8 im Zustand E.
Der Würfel, der in der 1. Runde in Z war, muss danach in den Zustand E wechseln, ansonsten ist die Bemalung aller restlichen Flächen in der 3. Runde nicht möglich. In der 3. Runde muss er auch im Zustand E sein. Aus demselben Grund muss der Würfel, der in der 2. bzw. 3. Runde in Z ist, vorher in E gewesen sein. Es ergibt sich ein Zyklus mit 3 Würfeln:
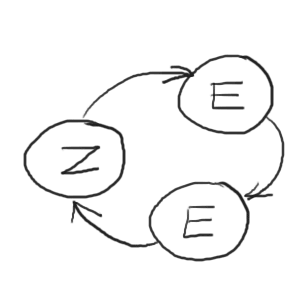
Ein Würfel, der in einer Runde in F ist (also 1 Fläche mit frischer Farbe hat), muss in den anderen beiden Runden die Zustände K und E durchlaufen, damit am Ende alle 6 Seiten bemalt sind.
Es gibt also 6 solcher Zyklen:
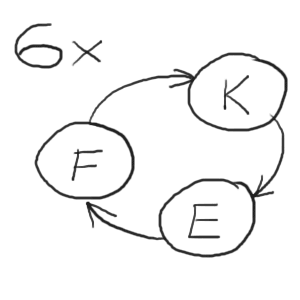
Damit sind jetzt 1× Z, 6× F, 8× E und 6× K belegt. Verbleiben noch 6 Würfel, die in jeder Runde im Zustand K sind:
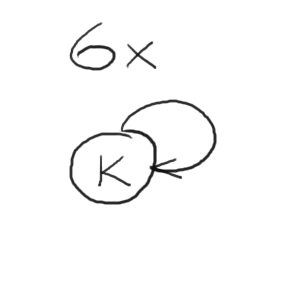
Beim Zusammensetzen des 3er-Würfels muss man freilich darauf achten, dass man die 1er-Würfel so dreht, dass die Bemalung der restlichen Flächen in späteren Runden noch möglich ist. (Nicht dass man bspw. nach der 2. Runde einen Würfel hat, bei dem 2 gegenüberliegende Flächen noch unbemalt sind.) Das ist aber immer möglich.
So, wo nun alle Würfel bemalt sind, geht’s an die Ostereier.
LLAP 🖖
“When UX doesn’t consider all users, shouldn’t it be known as ‘Some User Experience’ or... SUX? #a11y” —Billy Gregory


