Mathematik zum Wochenende
bearbeitet von@@Gunnar Bittersmann
Als Mittelpunkt einer Raumdiagonalen ist *P* natürlich Mittelpunkt des Würfels.
Zum Rechnen legen wir den Würfel so in ein Koordinatensystem, dass *H* im Ursprung liegt, *E* bei 1 auf der *x*-Achse, *G* bei 1 auf der *y*-Achse, *D* bei 1 auf der *z*-Achse. *P* ist (½, ½, ½).
Skizze[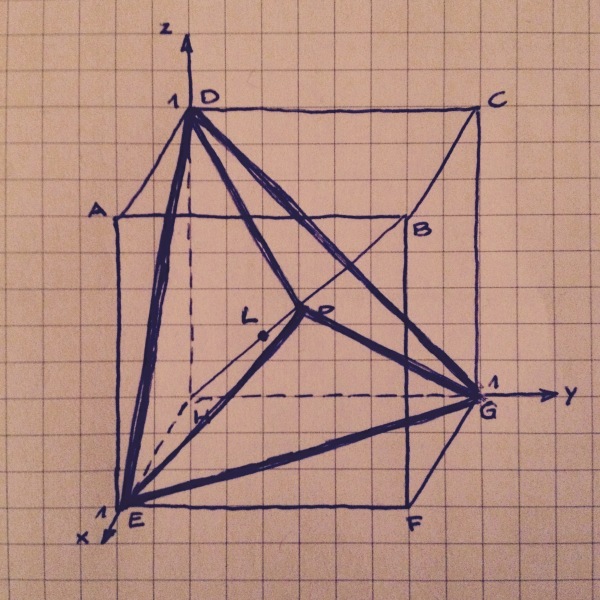](/images/f5c1bde5-baae-48bb-8adc-577740ec7174.jpeg)
Wir bestimmen den Schnittpunkt *L* der Raumdiagonalen *HB* mit der Ebene *DEG*. Das geht wohl am einfachsten über die Ebenengleichung *x* + *y* + *z* − 1 = 0 und *x* = *y* = *z* für alle Punkte der Geraden *HB*, wie @ottogal es gemacht hatte. (Ich hatte es über Vektoren gemacht.) *L* ist (⅓, ⅓, ⅓).
*LP* = ⅙√3, das ist die Höhe des Tetraeders *PDEG*. Dessen Grundfläche ist ein gleichseitiges Dreieck mit Kantenlänge √2, also mit Flächeninhalt ½√3.
Daraus ergibt sich das Volumendes Tetraeders *PDEG* zu ⅟₁₂.
---
Aber will man rechnen? Nein! @Friedel zeigt, wie’s ohne groß zu rechnen geht:
Der Tetraeder *PDEG* ist genau so groß wie die Tetraeder *PBDG*, *PBDE* und *PBEG*. Zusammen ergeben sie den Tetraeder *DGEB*. Die Tetraeder *HDEG*, *CBDG*, *ABDE* und *FBEG* sind auch gleichgroß. Zusammen mit *DGEB* ergeben sie den Würfel.
*HDEG*, *CBDG*, *ABDE* und *FBEG* haben jeweils ⅙ des Würfelvolumens. *DGEB* hat also das Volumen 1 − 4 ⋅ ⅙ = ⅓. Und ¼ davon ist ⅟₁₂.
*Chapeau!*{:@fr}
LLAP 🖖
--
“When UX doesn’t consider *all* users, shouldn’t it be known as ‘*Some* User Experience’ or... SUX? #a11y” —[Billy Gregory](https://twitter.com/thebillygregory/status/552466012713783297)
Mathematik zum Wochenende
bearbeitet von@@Gunnar Bittersmann
Als Mittelpunkt einer Raumdiagonalen ist *P* natürlich Mittelpunkt des Würfels.
Zum Rechnen legen wir den Würfel so in ein Koordinatensystem, dass *H* im Ursprung liegt, *E* bei 1 auf der *x*-Achse, *G* bei 1 auf der *y*-Achse, *D* bei 1 auf der *z*-Achse. *P* ist (½, ½, ½).
Skizze
Wir bestimmen den Schnittpunkt *L* der Raumdiagonalen *HB* mit der Ebene *DEG*. Das geht wohl am einfachsten über die Ebenengleichung *x* + *y* + *z* − 1 = 0 und *x* = *y* = *z* für alle Punkte der Geraden *HB*, wie @ottogal es gemacht hatte. (Ich hatte es über Vektoren gemacht.) *L* ist (⅓, ⅓, ⅓).
*LP* = ⅙√3, das ist die Höhe des Tetraeders *PDEG*. Dessen Grundfläche ist ein gleichseitiges Dreieck mit Kantenlänge √2, also mit Flächeninhalt ½√3.
Daraus ergibt sich das Volumendes Tetraeders *PDEG* zu ⅟₁₂.
---
Aber will man rechnen? Nein! @Friedel zeigt, wie’s ohne groß zu rechnen geht:
Der Tetraeder *PDEG* ist genau so groß wie die Tetraeder *PBDG*, *PBDE* und *PBEG*. Zusammen ergeben sie den Tetraeder *DGEB*. Die Tetraeder *HDEG*, *CBDG*, *ABDE* und *FBEG* sind auch gleichgroß. Zusammen mit *DGEB* ergeben sie den Würfel.
*HDEG*, *CBDG*, *ABDE* und *FBEG* haben jeweils ⅙ des Würfelvolumens. *DGEB* hat also das Volumen 1 − 4 ⋅ ⅙ = ⅓. Und ¼ davon ist ⅟₁₂.
*Chapeau!*{:@fr}
LLAP 🖖
--
“When UX doesn’t consider *all* users, shouldn’t it be known as ‘*Some* User Experience’ or... SUX? #a11y” —[Billy Gregory](https://twitter.com/thebillygregory/status/552466012713783297)


