@@Gunnar Bittersmann
Als Mittelpunkt einer Raumdiagonalen ist P natürlich Mittelpunkt des Würfels.
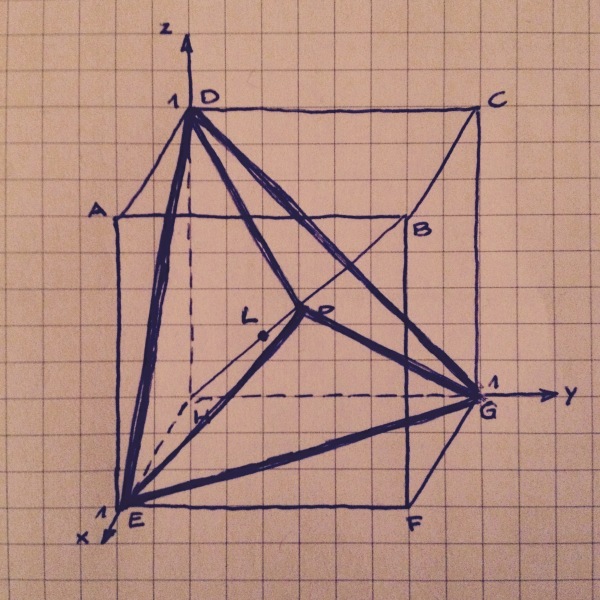
Zum Rechnen legen wir den Würfel so in ein Koordinatensystem, dass H im Ursprung liegt, E bei 1 auf der x-Achse, G bei 1 auf der y-Achse, D bei 1 auf der z-Achse. P ist (½, ½, ½).
Wir bestimmen den Schnittpunkt L der Raumdiagonalen HB mit der Ebene DEG. Das geht wohl am einfachsten über die Ebenengleichung x + y + z − 1 = 0 und x = y = z für alle Punkte der Geraden HB, wie @ottogal es gemacht hatte. (Ich hatte es über Vektoren gemacht.) L ist (⅓, ⅓, ⅓).
LP = ⅙√3, das ist die Höhe des Tetraeders PDEG. Dessen Grundfläche ist ein gleichseitiges Dreieck mit Kantenlänge √2, also mit Flächeninhalt ½√3.
Daraus ergibt sich das Volumendes Tetraeders PDEG zu ⅟₁₂.
Aber will man rechnen? Nein! @Friedel zeigt, wie’s ohne groß zu rechnen geht:
Der Tetraeder PDEG ist genau so groß wie die Tetraeder PBDG, PBDE und PBEG. Zusammen ergeben sie den Tetraeder DGEB. Die Tetraeder HDEG, CBDG, ABDE und FBEG sind auch gleichgroß. Zusammen mit DGEB ergeben sie den Würfel.
HDEG, CBDG, ABDE und FBEG haben jeweils ⅙ des Würfelvolumens. DGEB hat also das Volumen 1 − 4 ⋅ ⅙ = ⅓. Und ¼ davon ist ⅟₁₂.
Chapeau!
LLAP 🖖
“When UX doesn’t consider all users, shouldn’t it be known as ‘Some User Experience’ or... SUX? #a11y” —Billy Gregory