Mathematik zu Pfingsten - Lösungsvorschlag

[Matthias Apsel]

Hallo alle,

vielen Dank für die verschiedenen Lösungen, wer mag, kann das gern hier ergänzen.

Ich möchte eine Lösung vorstellen, die wenig kreativ ist und nur mit Mitteln der Analysis zum Ziel führt.

Zur Wiederholung:
Für ein gleichseitiges Dreieck gilt

$$h=\frac{\sqrt{3}}{2}\cdot a$$

$$A , = , \frac{\sqrt{3}}{4}\cdot a^2$$

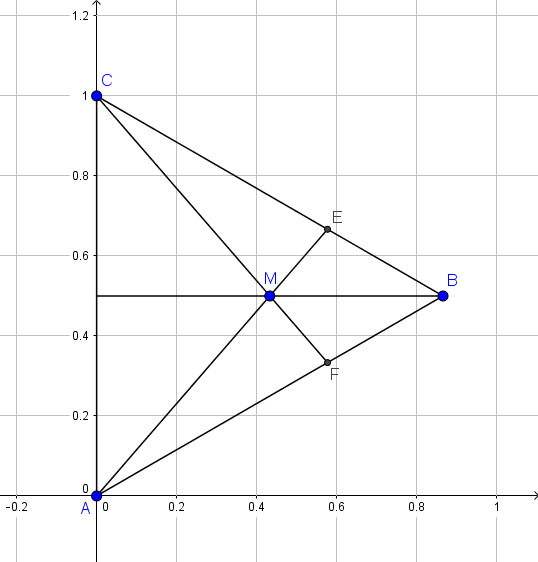
Der Einfachheit halber betrachten wir ein Dreieck mit der Seitenlänge 1, dessen Eckpunkte folgende Koordinaten haben $$\mathrm{A}\left(0\vert0\right), \mathrm{B}\left(\frac{\sqrt{3}}{2}\vert\frac{1}{2}\right), \mathrm{C}\left(0\vert1\right)$$.

Soll nun das gleichschenklige Dreieck drei Sechstel des Flächeninhaltes des gleichseitigen Dreiecks erhalten, so muss es die halbe Höhe besitzen. Der Punkt M halbiert also die Mittelsenkrechte. Er hat folglich die Koordinaten

$$\mathrm{M}\left(\frac{\sqrt{3}}{4}\vert\frac{1}{2}\right)$$

Wir wollen nun den Flächeninhalt des Drachenvierecks ausrechnen, dazu benötigen wir die Koordinaten von E.

Um den Punkt E zu ermitteln, brauchen wir die Gleichungen der Geraden durch die Punkte A und M sowie C und D. Diese lauten $$y=\frac{2}{3}\sqrt{3}\cdot x$$ und $$y=-\frac{1}{3}\sqrt{3}\cdot x+1$$.

Die Lösung des Gleichungssystems liefert $$\mathrm{E}\left(\frac{1}{3}\sqrt{3}\vert\frac{2}{3}\right)$$

Damit hat das Drachenviereck die Diagonalen $$e=\frac{1}{4}\sqrt{3}$$ sowie $$\frac{f}{2}=\frac{1}{6}$$. Der Flächeninhalt des Drachen ist folglich $$A=\frac{1}{2}ef= \frac{1}{24}\sqrt{3}$$, was einem Sechstel der Gesamtfläche des Dreiecks entspricht. Folglich haben die entsprechenden Flächen das angegebene Verhältnis.

MudGuards Einwurf:

Die Höhe des gleichligen Dreiecks muss ein Sechstel der Höhe des Dreiecks betragen. M hat somit die Koordinten $$\mathrm{M}\left(\frac{\sqrt{3}}{12}\vert\frac{1}{2}\right)$$, der Drachen eine Fläche von $$\frac{25}{168}\sqrt{3}$$, was einem Anteil von $$\frac{25}{42}\ne\frac{1}{2}$$ entspricht.

Bis demnächst
Matthias