Hallo Gunnar,
für den Fall dreier verschiedener Höhen $$h_1 < h_2 < h_3$$ habe ich noch eine Lösung, die ohne das Cavalieri-Prinzip auskommt.
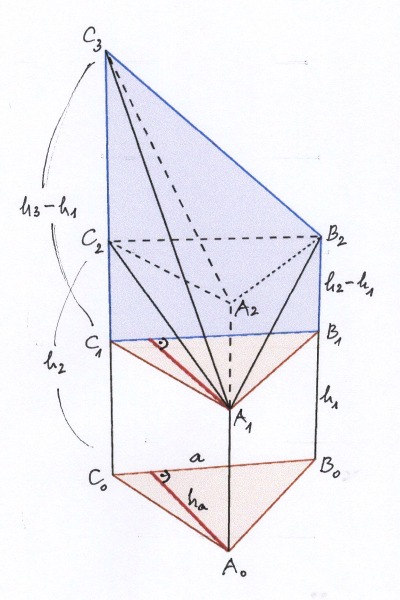
Man teilt wieder den Körper in der Höhe $$h_1$$ in ein Prisma unterhalb mit dem Volumen $$V_1 = A_G \cdot h_1$$ und den oberhalb liegenden Restkörper.
Dieser erweist sich als eine Pyramide mit trapezförmiger Grundfläche $$C_3C_1B_1B_2$$ und der Spitze $$A_1$$.
Die Höhe der Pyramide ist gleich der Dreieckshöhe $$h_a$$ auf die Seite $$a = B_0C_0$$ im Grunddreieck $$A_0B_0C_0$$; für diese gilt $$h_a = \frac{2A_G}{a}$$.
Das Trapez hat die Fläche $$A_T = \frac{(h_3 - h_1) + (h_2 - h_1)}{2} \cdot a = \frac{a}{2} \cdot (h_3 + h_2 - 2h_1)$$.
Damit erhält man das Volumen der Pyramide zu $$V_2 = \frac{1}{3}A_T \cdot h_a = \frac{A_T \cdot 2A_G}{3a} = A_G \cdot \frac{h_3 + h_2 - 2h_1}{3}$$.
Das Gesamtvolumen des Körpers ist daher $$V = V_1 + V_2 = A_G \cdot h_1 + A_G \cdot \frac{h_3 + h_2 - 2h_1}{3} = A_G \cdot \frac{h_1 + h_2 + h_3}{3}$$.
Viele Grüße
ottogal