Mathematik zum Wochenende – Lösung

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Die Aufgabe war eigentlich nicht schwer – wenn einem das räumliches Vorstellungsvermögen keinen Streich spielt. (Wir mir. 😧 Aber ich war in guter Gesellschaft. 😉)

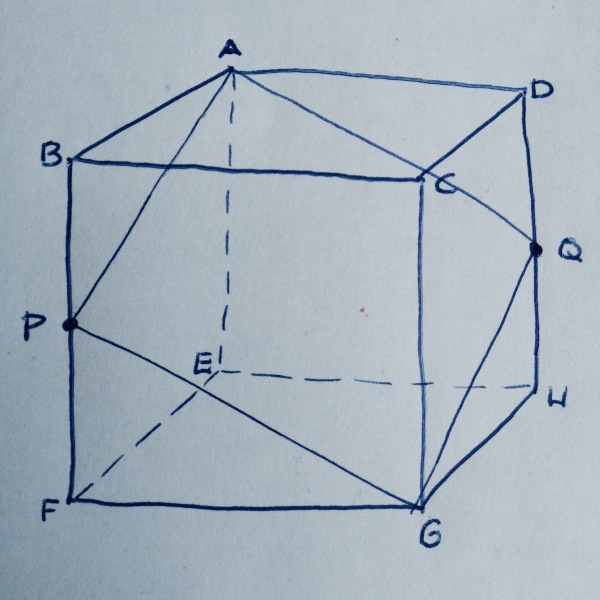
Gefragt war die Größe der Schnittfläche der Ebene AGP mit dem Würfel – und die beschränkt sich nicht auf das Dreieck AGP, sondern geht auf der anderen Seite der Raumdiagonalen AG weiter. Die Schnittfläche ist das Viereck AQGP (Q ist der Mittelpunkt der Kante DH). Alle Seiten sind Hypotenusen in rechtwinkligen Dreiecken mit den Kathetenlängen 1 und 2, also gleich lang; die Schnittfläche ist also ein Rhombus.

Die Fläche eines Drachenvierecks (was ein Rhombus ja ist) ist halb so groß wie die Fläche des Rechtecks aus seinen Diagonalen. Die eine Diagonale AG ist die Raumdiagonale des Würfels, also 2√3 lang. Die andere Diagonale PQ ist so lang wie die Diagonale der Seitenflächen, also 2√2. Die Schnittfläche ist also ½ ⋅ 2√3 ⋅ 2√2 = 2√6. (@ottogal und @Tabellenkalk hatten’s so.)

Andere Möglichkeit: Koordinatensystem mit A als Ursprung, B auf x-Achse, D auf y-Achse, E auf z-Achse. P hat darin die Koordinaten (2, 0, 1), Q die Koordinaten (0, 2, 1). Die Fläche des von den Vektoren AP und AQ aufgespannten Parallelogramms (was ein Rhombus ja ist) ist |AP × AQ|.

$$\begin{align} \overrightarrow{AP} \times \overrightarrow{AQ} &= \begin{vmatrix} \overrightarrow{e_x} & \overrightarrow{e_y} & \overrightarrow{e_z}
2 & 0 & 1
0 & 2 & 1\end{vmatrix} = \begin{pmatrix} -2 \ -2 \ 4\end{pmatrix}
\vert \overrightarrow{AP} \times \overrightarrow{AQ} \vert &= \sqrt{4+4+16} = \sqrt{4} \cdot \sqrt{1+1+4} = 2 \sqrt{6} \end{align}$$

Noch eine Möglichkeit (so hatte ich’s zuerst gemacht): Die Schnittfläche ist doppelt so groß wie das Dreieck AGP; dessen Fläche berechnet sich aus den Seitenlängen 2√3, √5 und √5 nach der heronischen Formel:

$$\begin{align} s &= \sqrt{5} + \sqrt{3}
A_{AGP} &= \sqrt{ \left( \sqrt{5} + \sqrt{3} \right) \cdot \left( \sqrt{5} - \sqrt{3} \right) \cdot \sqrt{3} \cdot \sqrt{3}} = \sqrt{ \left( 5 - 3 \right) \cdot 3} = \sqrt{6}
A_{AQGP} &= 2\sqrt{6} \end{align}$$

---

Was ist denn mit der anderen Aufgabe? Will keiner? Braucht ihr einen Tip? Ich hab’s über Winkelfunktionen gelöst. Aber auch nicht auf Anhieb am ersten Tag.

LLAP 🖖