noch mehr Mathematik zum Wochenende – Lösung

[Gunnar Bittersmann]

@@Gunnar Bittersmann

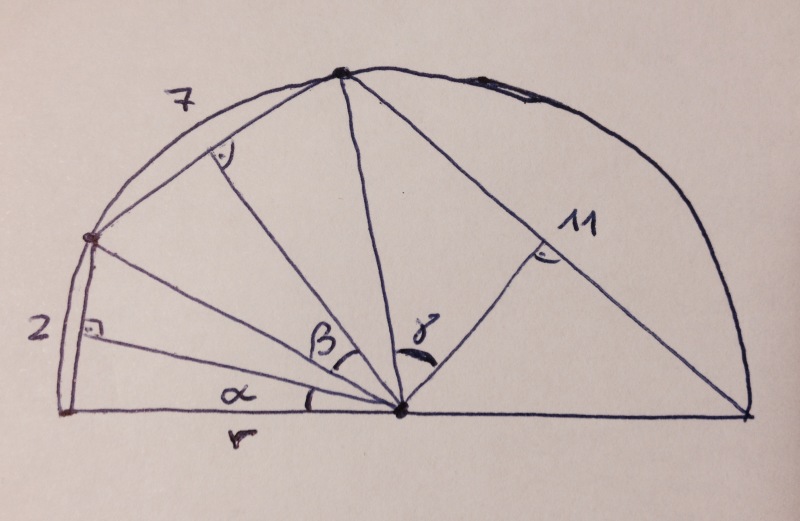
Stellen wir uns das mal räumlich vor – als Pizza. Dass deren Volumen bei Radius z und Dicke a gleich pi z z a ist, tut hier nichts zur Sache. Wir können bei der Benennung r für den Radius bleiben. Selbstredend r > 0; Pizzateig wird ja aus- und nicht eingerollt.

Wir schneiden die Pizza so in 6 Stücke (immer schön durch die Mitte), dass die Sehnen entsprechende Längen haben. Nun können wir die Stücken auch vertauschen: 2, 7, 11, 2, 7, 11 – wir haben immer noch die ganze Pizza kreisrund auf dem Tisch. Nur dass wir die Hälfte davon zur Lösung der Aufgabe nicht mehr brauchen. Der Hund unterm Tisch freut sich. 🐶

Wir behalten nur ein großes, ein mittleres und ein kleines Stück. Diese teilen wir in der Mitte nochmal. Der Zentriwinkel der kleinen Hälften sei α, der der mittleren β und der der großen γ.

Dann ist

$$\begin{align} \sin \alpha &= \frac{1}{r}
\sin \beta &= \frac{7}{2r}
\sin \gamma &= \frac{11}{2r}
\alpha + \beta + \gamma &= \tfrac{1}{2} \pi \qquad \alpha + \beta = \tfrac{1}{2} \pi - \gamma \end{align}$$

Ein Gleichungssystem mit 4 Gleichungen und 4 Unbekannten – das sollte zu lösen sein.

Cowinkelbeziehung:

$$\sin \gamma = \cos \left( \tfrac{1}{2} \pi - \gamma \right) = \cos \left( \alpha + \beta \right) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \quad (*)$$

Wir brauchen noch die Cosinüsse:

$$\begin{align} \cos \alpha &= \sqrt{1 - \sin^2 \alpha} = \frac{\sqrt{r^2 -1}}{r}
\cos \beta &= \sqrt{1 - \sin^2 \beta} = \frac{\sqrt{4r^2 -49}}{2r} \end{align}$$

Alles in (*) eingesetzt:

$$\begin{align} \frac{11}{2r} &= \frac{\sqrt{r^2 -1}}{r} \frac{\sqrt{4r^2 -49}}{2r} - \frac{1}{r} \frac{7}{2r}
11r &= \sqrt{r^2 -1} \sqrt{4r^2 - 49} - 7
11r + 7 &= \sqrt{r^2 -1} \sqrt{4r^2 - 49}
\left( 11r + 7 \right)^2 &= \left( r^2 -1 \right) \left( 4r^2 - 49 \right)
121r^2 + 154r + 49 &= 4r^4 -53r^2 + 49
0 &= 4r^4 - 174r^2 - 154r
0 & = 2r^3 - 87r - 77
\end{align}$$

Durch Probieren findet man die ganzzahlige Lösung r₁ = 7. (Schwein gehabt.)

Polynomdivision:

$$\begin{align} \left( 2r^3 - 87r -77 \right) : \left( r - 7 \right) &= 2r^2 + 14r + 11
0 &= r^2 + 7r + \tfrac{11}{2}
r_{2,3} &= -\tfrac{7}{2} \pm \sqrt{\tfrac{49}{4} - \tfrac{22}{4}} = -\tfrac{7}{2} \pm \tfrac{\sqrt{27}}{2} < 0 \end{align}$$

Die anderen beiden Lösungen fallen also als Werte für r aus.

Bleibt übrig: r = 7 – und die halbe Pizza. Die können wir jetzt auch dem Hund geben – oder selber essen. Wohl bekomm’s! 🍕

LLAP 🖖