Mathematik zum Wochenende – Lösung

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Hm, Kreise scheinen hier nicht so gut anzukommen. Wie so oft bei Geometriaufgaben ist die richtige Hilfslinie schon die halbe Lösung.

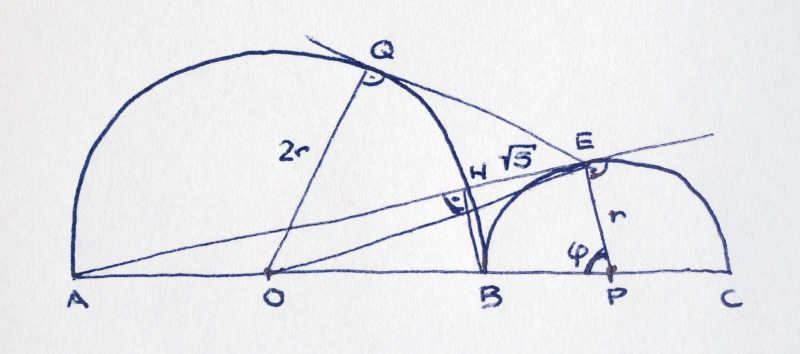
O sei der Mittelpunkt des großen Kreises mit dem Raduis 2r; P der Mittelpunkt des kleinen Kreises mit dem Raduis r.

An EQ kommt man über das Dreieck OEQ:

EQ² = OE² − OQ² = OE² − 4r²

An OE kommt man über das Dreieck OPE:

OE² = OP² + PE² − 2 OP PE cos ϕ = 9r² + r² − 2 ⋅ 3r ⋅ r cos ϕ = 10r² − 6r² cos ϕ

An cos ϕ kommt man über das Dreieck APE:

cos ϕ = PE / AP = r / 5r = ⅕

Eingesetzt:

EQ² = 10r² − 6r² ⋅ ⅕ − 4r² = ²⁴⁄₅r²

Brauchen wir nur noch den Radius. Da kommt die Länge von HE ins Spiel.

Winkel BHA ist ebenso wie PEA rechtwinklig (Thales). Strahlensatz:

AE / HE = AE / √5 = AP / BP = 5r / r = 5
AE = 5√5

AE² = 125 = AP² − PE² = 25r² − r² = 24r²
r² = ¹²⁵⁄₂₄

EQ² = ²⁴⁄₅ ⋅ ¹²⁵⁄₂₄ = 25
EQ = 5

LLAP 🖖