Mathematik zum Wochenende – Lösung

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Wo nun schon das übernächste Wochenende ansteht, wird’s mal Zeit für die Lösung. Oder erstmal meinen Lösungsversuch, den ich euch nicht vorenthalten möchte:

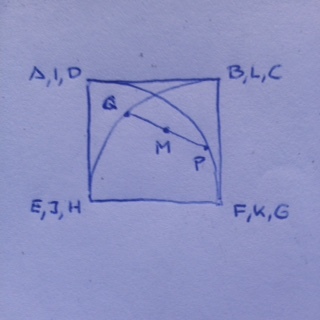
Zunächst einmal lässt sich das Problem von 3D auf 2D reduzieren – auf die Ebene IJKL (in der auch M liegt). Die Projektionen von P und Q auf diese Ebene liegen auf Kreisbögen um J bzw. K mit dem Radius einer Kantenlänge a des Quadrats IJKL.

Dann hatte ich mir die Extreme für einen Punkt rausgepickt: Wenn Q in J liegt und P seinen Viertelkreisbogen durchwandert, dann beschreibt M einen Viertelkreis um J mit dem Radius ½a. Wenn Q in L liegt und P seinen Viertelkreisbogen durchwandert, dann beschreibt M einen Viertelkreis um den Mittelpunkt des Quadrats mit dem Radius ½a.

Die Fläche, die M überstreichen kann, sollte also aussehen – dachte ich:

Bis die erste Lösung eines anderen bei mir eintraf. Ja natürlich! Da hätte ich Trottel auch durch zwei Sekunden Nachdenken drauf kommen können. Das kann ja gar nicht stimmen! Warum nicht?

Sehen wir und die Aufgabe nochmal an:

Die Aufgabe ist symmetrisch bezüglich der eingezeichneten Achse. Also muss auch die Lösung dazu symmetrisch sein.

(Diese Erkenntnis ist es, warum ich meinen Irrweg hier aufschrieb.)

Man muss obige Überlegung auch noch für P anstellen und Q seinen Viertelkreisbogen durchlaufen lassen:

Die Lösung ergibt sich aus dem Durchschnitt beider Mengen:

@ottogal hat das mit GeoGebra sehr schön visualisiert: in 3D • mit Spur und Animation • in 2D.

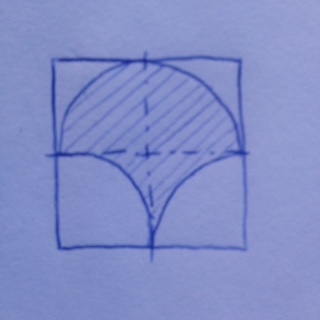
Zur Flächenberechnung nun nicht irgendwas mit π rummachen, sondern erstmal hinschauen: die Viertelkreise aus der oberen Hälfte passen genau in die weißen Flächen in der unteren Hälfte. Die schraffierte Fläche bedeckt also die Hälfte des Quadrats. Für a = 8 cm ist sie also ½a² = 32 cm².

LLAP 🖖