Mathematik zum Wochenende

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Wo ich meine Lösung schon abschickbereit im Editor hatte, will ich sie auch noch in die Runde werfen. Die zu Aufgabe 1 ähnelt der von Rolf (wo er von „Symmetrie an Drachen“ spricht, spreche ich von kongruenten Dreiecken) und scheint mir einfacher als die von ottogal.

ottogals Lösung zur Aufgabe 2 scheint mir sehr elegant. – Sich auf eine Lösung zu einer vorherigen Aufgabe zu beziehen schien mir aber auch elegant. 😉

#Aufgabe 1

Wie immer™ kommt es auf das Einzeichnen der richtigen Hilfslinien an:

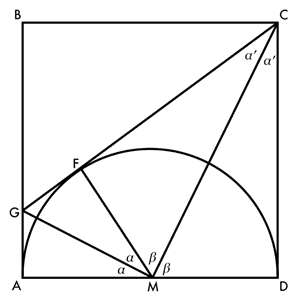
M Mittelpunkt des Halbkreises, o.B.d.A. Seitenlänge des Quadrats: 1.

MC ≡ MC, MF = MD = ½ (Radien), ∡MFC = ∡MDC = 1∟ ⇒ △CFM ≅ △CDM (SSW) ⇒ CF = CD = 1.

MG ≡ MG, MA = MF = ½ (Radien), ∡MAG = ∡MFG = 1∟ ⇒ △GAM ≅ △GFM (SSW) ⇒ GA = GF.

Seien α = ∡AMG = ∡FMG, α′ = ∡FCM = ∡DCM, β = ∡CMF = ∡CMD.

Gestreckter Winkel: 2α + 2β = 2∟, also α + β = 1∟.

Wegen Innenwinkelsumme α′ + β + 1∟ = 2∟, also α′ + β = 1∟, folglich α′ = α ⇒ △GAM ∼ △CDM.

GA : MA = GA : ½ = MD : CD = 1 : 2 ⇒ GA = GF = ¼.

BG : BC : CG = (1 − ¼) : 1 : (1 + ¼) = 3 : 4 : 5.

#Aufgabe 2

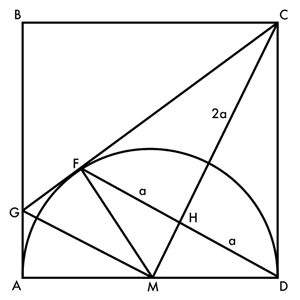
Und noch eine Hilfslinie mehr: FD schneidet MC in H.

HC ≡ HC, CF = CD = 1, ∡HCF = ∡HCD (s.o.) ⇒ △CHF ≅ △CHD (SSW) ⇒ ∡FHC = ∡DHC = 1∟.

Damit ist △CHD ∼ △CDM ⇒ CH :DH = CD : MD = 2 : 1. Sei DH = a, CH = 2a.

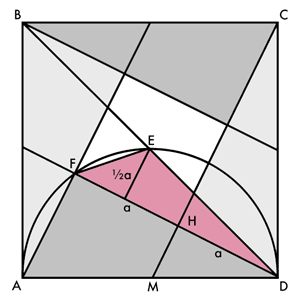
Wir erinnern uns an @encoder⁠s Plan und zerlegen das Quadrat in 4 kongruente Dreiecke mit den Seitenlängen a und 2a und ein Quadrat mit der Seitenlänge a.

Die Fläche ABCD ist 4 × ½a × 2a + a² = 5a² = 1, also a² = ⅕. Und nein, wir ziehen hier nicht die Wurzel.

Da E Mittlepunkt der Figur ist, ist die Höhe des Dreiecks DEF zur Grundseite FD gleich ½a, seine Fläche folglich ½ × 2a × ½a = ½a² = ⅟₁₀. Das ist dann auch das gesuchte Verhältnis zur Fläche ABCD.

LLAP 🖖