Geometrie zum Wochenende
- mathematik
Oder: zum Sonntag. Für die Aufgabe sollte man nicht das ganze Wochenende brauchen.
Wenn die Fläche des Zweiecks 4 ist, wie groß ist die blau gemalte Fläche?
LLAP 🖖
Hallo Gunnar Bittersmann,
Oder: zum Sonntag. Für die Aufgabe sollte man nicht das ganze Wochenende brauchen.
Ich hab noch ein bisschen für den Vormittag:
Gegeben ist ein regelmäßiges sechsseitiges Prisma mit quadratischen Seitenflächen. Dieses wird durch eine Ebene geschnitten, die durch zwei gegenüberliegende parallele Seitenkanten des Prismas verläuft.
Berechne die Größe der Schnittfläche.
Bis demnächst
Matthias
Da hab ich grad die Lösung von Gunnars Aufgabe an ihn geschickt und gedacht, der Rest-Sonntag sei nun mathefrei... (Zum Glück backt meine Frau heute Stollen...)
Hallo ottogal,
(Zum Glück backt meine Frau heute Stollen...)
Dann kann ich ja noch eine Zusatzaufgabe nachschieben. Welche Höhe muss das Prisma haben, damit die sechseckige Schnittfläche doppelt so groß wie die Grundfläche des Prismas ist?
Bis demnächst
Matthias
Tach!
(Zum Glück backt meine Frau heute Stollen...)
Dann kann ich ja noch eine Zusatzaufgabe nachschieben. Welche Höhe muss das Prisma haben, damit die sechseckige Schnittfläche doppelt so groß wie die Grundfläche des Prismas ist?
Die eigentliche Frage ist doch, eignet sich das Gefäß nach einem derartigen Durchschneiden noch zum Aufbewahren von Stollenbackzutaten?
dedlfix.
Hi,
Gegeben ist ein regelmäßiges sechsseitiges Prisma mit quadratischen Seitenflächen. Dieses wird durch eine Ebene geschnitten, die durch zwei gegenüberliegende parallele Seitenkanten des Prismas verläuft.
Berechne die Größe der Schnittfläche.
42
Die zugehörige Kantenlänge zu ermitteln, überlasse ich den Lesern zur Übung 😉
cu,
Andreas a/k/a MudGuard
Hallo Matthias Apsel,
Gegeben ist ein regelmäßiges sechsseitiges Prisma mit quadratischen Seitenflächen. Dieses wird durch eine Ebene geschnitten, die durch zwei gegenüberliegende parallele Seitenkanten des Prismas verläuft.
Berechne die Größe der Schnittfläche.
@ottogal wies darauf hin, dass die Schnittfläche so nicht eindeutig beschrieben ist.
Der Flächeninhalt dieser Schnittfläche ist 2_a_², falls die Länge der Seitenkanten mit a bezeichnet wird.
Die andere Schnittfläche ist ein Sechseck, das sich in 12 kongruente Dreiecke zerlegen lässt. (@ottogal)
Jedes dieser Dreiecke hat den Flächeninhalt $$\frac{1}{2} \cdot \frac{1}{2}a \cdot a = \frac{1}{4}a²$$, die Schnittfläche also den Inhalt $$3a²$$.
@Rolf B und ich haben die Schnittfläche als zwei Trapeze angesehen.
@Gunnar Bittersmann hat einen Lösungsweg von eleganter Effizienz vorgelegt.
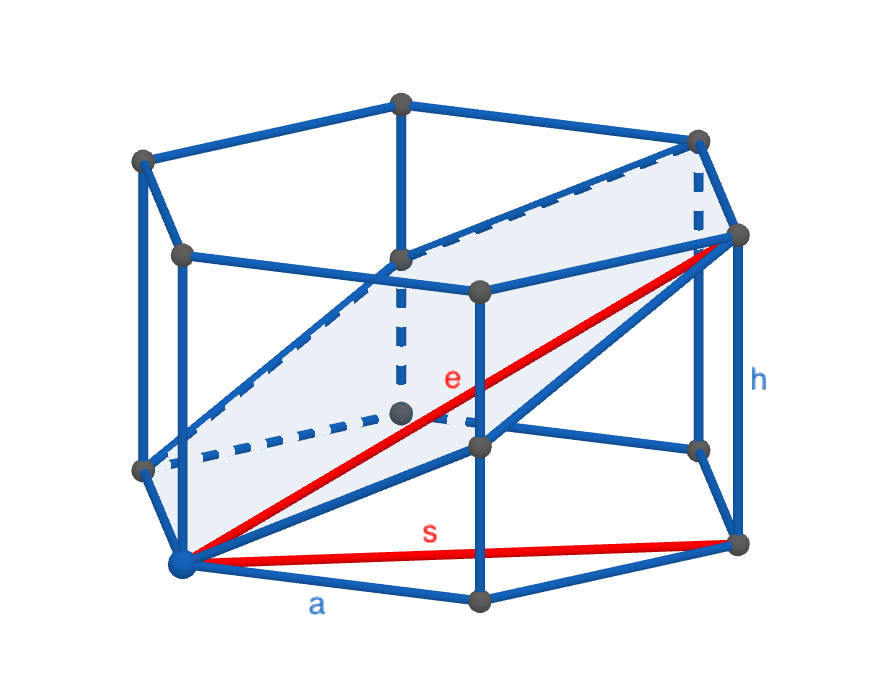
Die Schnittfläche ist ein Sechseck, das aus dem regulären Sechseck durch Streckung in eine Richtung um den Faktor e/s hervorgeht. Mit s = a √3 und h = a ergibt sich e² = s² + h² = 4a², folglich e = 2a.
Der Flächeninhalt der Schnittfläche ist dann auch das e/s-fache der Grundfläche, also 2/√3 × ³⁄₂a² √3 = 3a².
Zusatzaufgabe: Wenn die Schnittfläche doppelt so groß ist wie die Grundfläche ist, gilt e = 2s und damit h² = e² − s² = 3s², also h = s √3 = 3a.
Bis demnächst
Matthias
@@Matthias Apsel
Meh, warum sieht das so aus? Ich hatte extra in den Gleichungen NBSP gesetzt, damit darin kein Zeilenumbruch stattfindet, sondern die ganze Gleichung in die neue Zeile rutscht. Es sollte so aussehen wie in der DM an Matthias:
Irgendwie gehen die NBSP bei Kopieren/Einfügen verloren (d.h. sie werden durch normale Leerzeichen ersetzt). Warum das? Und lässt sich das beheben, @Christian Kruse?
LLAP 🖖
Hallo Gunnar,
Irgendwie gehen die NBSP bei Kopieren/Einfügen verloren (d.h. sie werden durch normale Leerzeichen ersetzt). Warum das? Und lässt sich das beheben, @Christian Kruse?
Nein. Ist yet another Firefox-Bug, der vermutlich nie behoben werden wird. Mit Chrome gehts wie erwartet.
LG,
CK
@@Gunnar Bittersmann
Wenn die Fläche des Zweiecks 4 ist, wie groß ist die blau gemalte Fläche?
Ein Chapeau! an @beatovich für: „Unter der Annahme, dass die Anzahl der definierten Punkte 4 ist und der einzige definierte Winkel ein Vollkreis durch 4 ist, gibt es keinen Grund an eine andere Zahl zu denken.“
Ich hatte noch überlegt, ob ich bei der Aufgabe dazuschreiben sollte, dass in der Herleitung nirgendwo π auftauchen sollte; dachte aber dann: ach, mal sehen, was so reinkommt. 😜
Es kamen einige Lösungen rein, in denen die Flächen von Viertelkreisen und Quadrat aneinandergelegt und abgeschnitten wurden.
Ich hatte mich auf die Kreissegmente beschränkt:
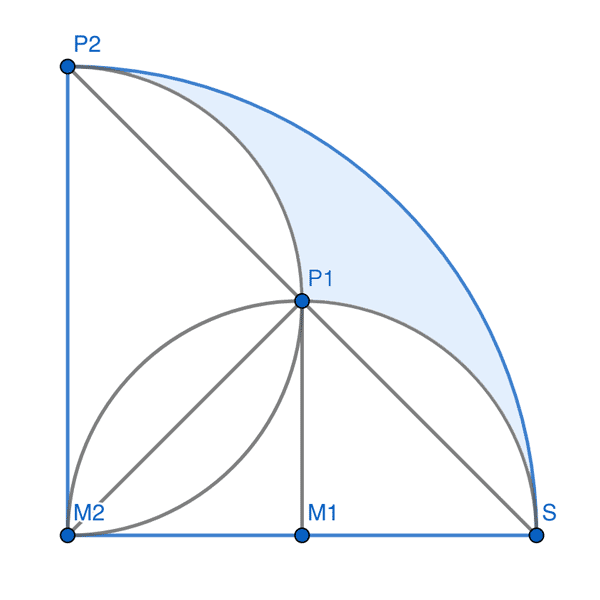
Die Kreissegmente ⌓P₁P₂ und ⌓SP₁ sind kongruent zu ⌓M₂P₁; sie haben alle die Fläche 2. Mit S als Zentrum führt die Streckung von M₁ und P₁ um den Faktor k = 2 zu M₂ und P₂. Die Fläche von ⌓SP₂ ist damit k² = 4 Mal so groß wie die von ⌓SP₁, also 8. Blaue Fläche: 8 − 2 × 2 = 4.
LLAP 🖖
Ich hatte noch überlegt, ob ich bei der Aufgabe dazuschreiben sollte, dass in der Herleitung nirgendwo π auftauchen sollte; dachte aber dann: ach, mal sehen, was so reinkommt. 😜
Meine Lösung ohne π:
Da der große Kreisradius das Doppelte des kleinen ist, ist die Gesamtfläche das Vierfache des kleinen Viertelkreises, also $$4A_3$$.
Ferner gilt $$A_3=A_1+A_4$$ und somit für die Fläche des Quadrats: $$A_{Qu}=A_3+A_4$$.
Damit erhält man
$$A_2=A_{ges}-2A_3-A_{Qu}=4A_3-2A_3-(A_3+A_4)=A_3-A_4=A_1.$$
Also ist auch $$A_2=4$$.
Hallo Gunnar,
die Idee mit der Streckung war nicht schlecht. Ich glaube, meine Argumentation entspricht der von Ottogal, ist nur etwas anders notiert. Und gut, dass Gunnar das Pi-Verbot nicht erwähnte 😀, mit sind nämlich die Hilfslinien nicht aufgefallen, die sichtbar machen, dass die Halbkreise die halbe Fläche des großen Viertelkreises haben.
Mein Weg zu dieser Erkenntnis war dieser: Der große Viertelkreis hat die Fläche $$\frac{1}{4}\pi r^2$$. Die Halbkreise haben die Fläche $$\frac{1}{2}\pi(\frac{r}{2})^2 = \frac{1}{8}\pi r^2$$. Davon haben wir zwei, d.h. die Fläche der Halbkreise, ohne Beachtung der Überlappung addiert, ist genauso groß wie der Viertelkreis.
Nachdem man auf welchem Weg auch immer darauf gekommen ist, dass die Flächensumme der Halbkreise gleich der Fläche des Viertelkreises ist, ist ohne weitere Rechnung offensichtlich, dass bei einer Überlappung der Halbkreise um X Quadratgunnars die gleiche Fläche im Viertelkreis frei bleibt.
Rolf
Nachdem man auf welchem Weg auch immer darauf gekommen ist, dass die Flächensumme der Halbkreise gleich der Fläche des Viertelkreises ist, ist ohne weitere Rechnung offensichtlich, dass bei einer Überlappung der Halbkreise um X Quadratgunnars die gleiche Fläche im Viertelkreis frei bleibt.
Guter Gedanke!
hallo
@@Gunnar Bittersmann
Wenn die Fläche des Zweiecks 4 ist, wie groß ist die blau gemalte Fläche?
Ein Chapeau! an @beatovich für: „Unter der Annahme, dass die Anzahl der definierten Punkte 4 ist und der einzige definierte Winkel ein Vollkreis durch 4 ist, gibt es keinen Grund an eine andere Zahl zu denken.“
Ich hatte noch überlegt, ob ich bei der Aufgabe dazuschreiben sollte, dass in der Herleitung nirgendwo π auftauchen sollte; dachte aber dann: ach, mal sehen, was so reinkommt. 😜
Du hättest den Flächeninhalt mit π beschreiben können. Das hätte mindestens die Form der Antwort erschwert.
Die Lösung kann intuitiv verstanden werden anhand eines Quadrates, dessen 4 Teilquadrate alle gleich gross sind.
A|0 AB|B
@@beatovich
A|0 AB|B
Blutgruppen?
LLAP 🖖