Geometrie zum Wochenende – Lösung

[ottogal]

Ich hatte noch überlegt, ob ich bei der Aufgabe dazuschreiben sollte, dass in der Herleitung nirgendwo π auftauchen sollte; dachte aber dann: ach, mal sehen, was so reinkommt. 😜

Meine Lösung ohne π:

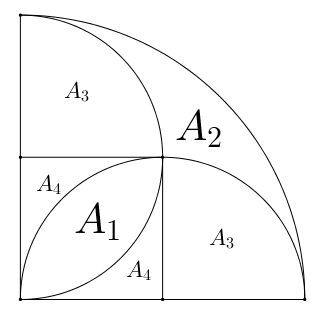
Da der große Kreisradius das Doppelte des kleinen ist, ist die Gesamtfläche das Vierfache des kleinen Viertelkreises, also $$4A_3$$.
Ferner gilt $$A_3=A_1+A_4$$ und somit für die Fläche des Quadrats: $$A_{Qu}=A_3+A_4$$.

Damit erhält man
$$A_2=A_{ges}-2A_3-A_{Qu}=4A_3-2A_3-(A_3+A_4)=A_3-A_4=A_1.$$
Also ist auch $$A_2=4$$.