Geometrie zum Wochenende - Lösung

[Matthias Apsel]

Hallo Matthias Apsel,

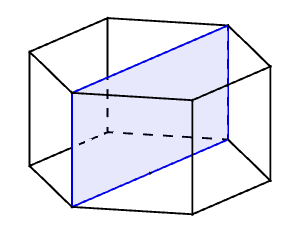
Gegeben ist ein regelmäßiges sechsseitiges Prisma mit quadratischen Seitenflächen. Dieses wird durch eine Ebene geschnitten, die durch zwei gegenüberliegende parallele Seitenkanten des Prismas verläuft.
Berechne die Größe der Schnittfläche.

@ottogal wies darauf hin, dass die Schnittfläche so nicht eindeutig beschrieben ist.

Der Flächeninhalt dieser Schnittfläche ist 2_a_², falls die Länge der Seitenkanten mit a bezeichnet wird.

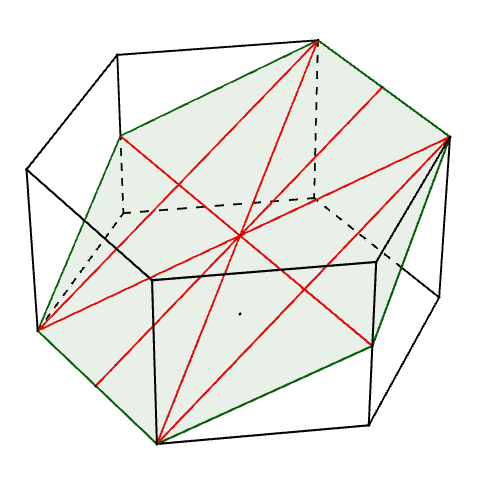
Die andere Schnittfläche ist ein Sechseck, das sich in 12 kongruente Dreiecke zerlegen lässt. (@ottogal)

Jedes dieser Dreiecke hat den Flächeninhalt $$\frac{1}{2} \cdot \frac{1}{2}a \cdot a = \frac{1}{4}a²$$, die Schnittfläche also den Inhalt $$3a²$$.

@Rolf B und ich haben die Schnittfläche als zwei Trapeze angesehen.

@Gunnar Bittersmann hat einen Lösungsweg von eleganter Effizienz vorgelegt.

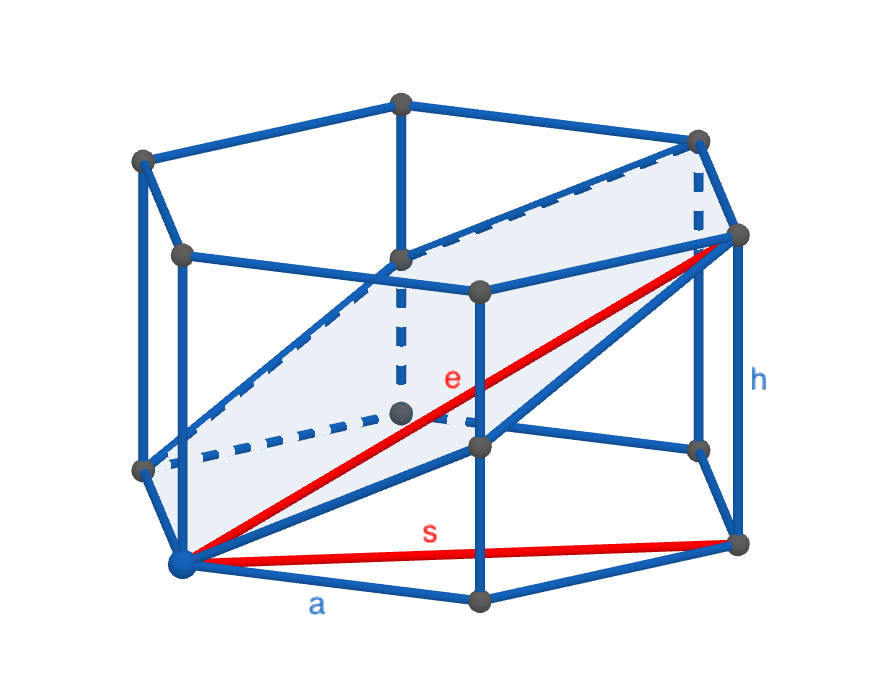
Die Schnittfläche ist ein Sechseck, das aus dem regulären Sechseck durch Streckung in eine Richtung um den Faktor e/s hervorgeht. Mit s = a √3 und h = a ergibt sich e² = s² + h² = 4a², folglich e = 2a.

Der Flächeninhalt der Schnittfläche ist dann auch das e/s-fache der Grundfläche, also 2/√3 × ³⁄₂a² √3 = 3a².

Zusatzaufgabe: Wenn die Schnittfläche doppelt so groß ist wie die Grundfläche ist, gilt e = 2s und damit h² = e² − s² = 3s², also h = s √3 = 3a.

Bis demnächst
Matthias