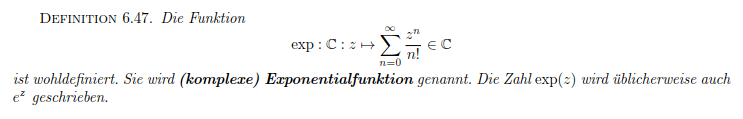Wie nennt sich das?

[Camping_RIDER]

Aloha ;)

Auch $$e$$ und $$\pi$$ haben, genau wie die imaginäre Einheit $$i$$, nur den Charakter einer Definition:

?? „Nur den Charakter“?

Ich verstehe unter „den Charakter einer Definition haben“, dass ein Begriff in Form einer Definition geprägt wird, so wie andere Begriffe in Form von Sätzen geprägt werden.

Die Formulierung $$e$$ ist eine Definition ist genauso unsauber, denn $$e$$ selbst ist keine Definition, sondern ein Begriff, der im Rahmen einer Definition geprägt wird.

Ich habe mich deshalb für diese Formulierung entschieden.

$$e$$ ist der Grenzwert einer Reihe

Ich hätte gedacht, einer Folge. $$\left( 1 + \frac{1}{n} \right)^n$$

Es gibt unterschiedliche, äquivalente Möglichkeiten, die selbe Zahl zu definieren.

Aber laut Wikipedia ist e tatsächlich definiert als Grenzwert einer Reihe.

Deshalb steht die Definition über den Grenzwert der Folge in Wikipedia unter dem Stichwort ebenfalls auch mit dabei.

$$\pi$$ ist das Doppelte der kleinsten positiven Nullstelle einer Funktion namens Kosinus, die ihrerseits über eine Taylorreihe definiert ist.

π ist definiert als Verhältnis des Umfangs eines Kreises zu dessen Durchmesser.

Es gibt unterschiedliche, äquivalente Möglichkeiten, die selbe Zahl zu definieren. In der Mathematik sind die Begriffe Kreis und Durchmesser nur in einem kleinen Teilgebiet relevant und definiert (nämlich in der Geometrie), weshalb man für $$\pi$$, das ja auch in vielen anderen Teilgebieten, allen voran in der Analysis, Bedeutung besitzt, für gewöhnlich eine andere - nämlich die genannte - Definition.

Ich zitiere als Referenz dazu gerne mein Analysis-1-Skript:

Grüße,

RIDER