@@Gunnar Bittersmann
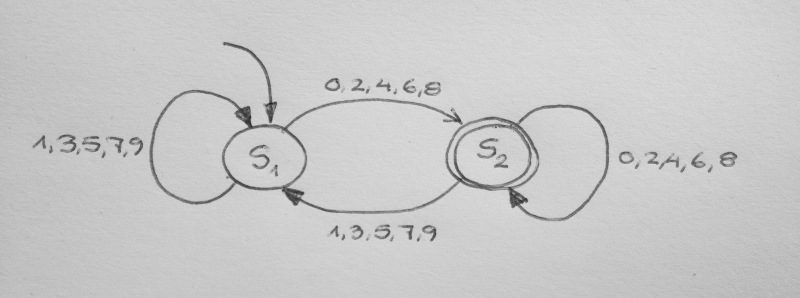
Das Bild zeigt einen endlichen Automaten, der sich bei der Eingabe einer Ziffernfolge nur dann im Endzustand (dargestellt durch doppelte Linie) befindet, wenn die dadurch eingegebene Zahl durch 2 teilbar ist. (Führende Nullen sollen erlaubt sein.)
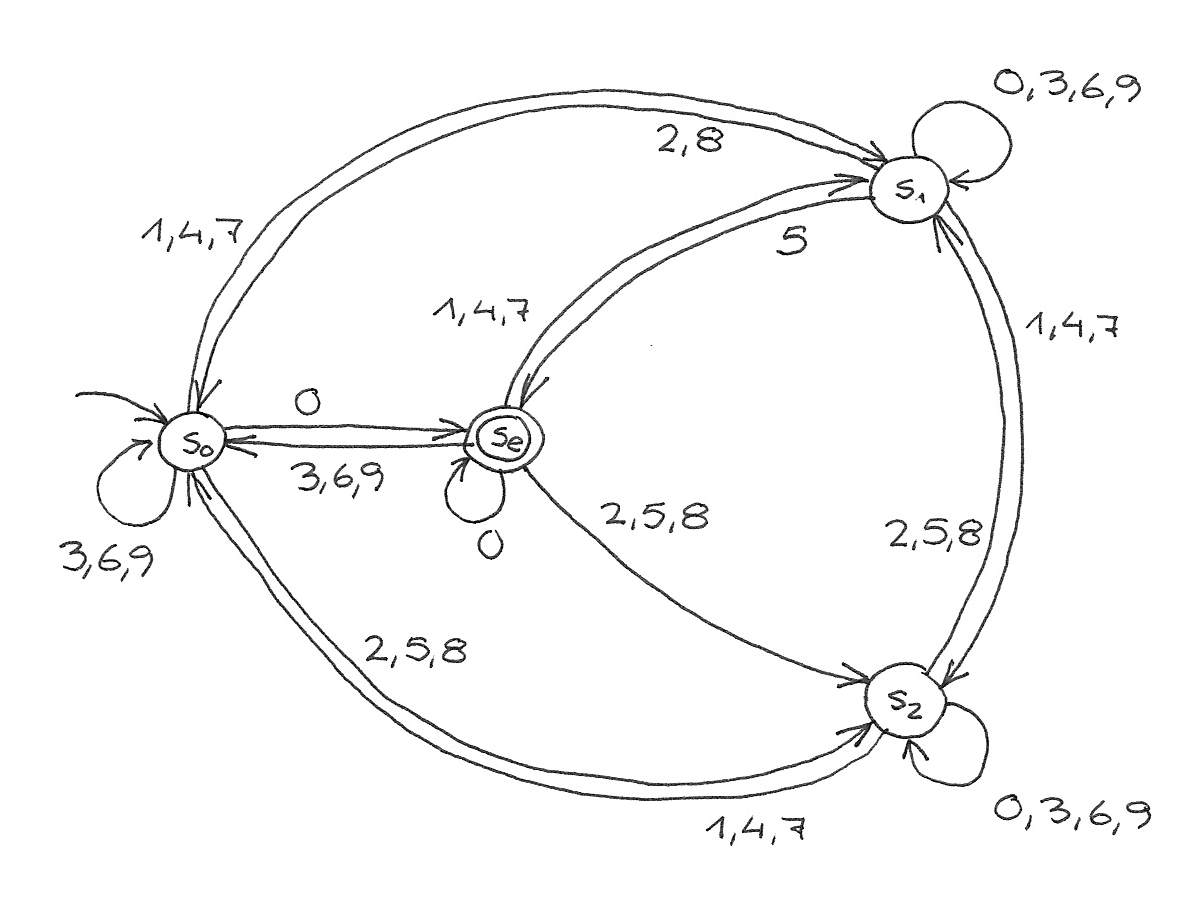
Baue einen endlichen Automaten, der sich nur dann in einem Endzustand befindet, wenn die eingegebene Zahl durch 3 teilbar ist.
Man könnte geneigt sein zu denken: Teilbarkeit durch 2 – 2 Zustände, Teilbarkeit durch 3 – 3 Zustände, und kommt auf diesen Automaten:
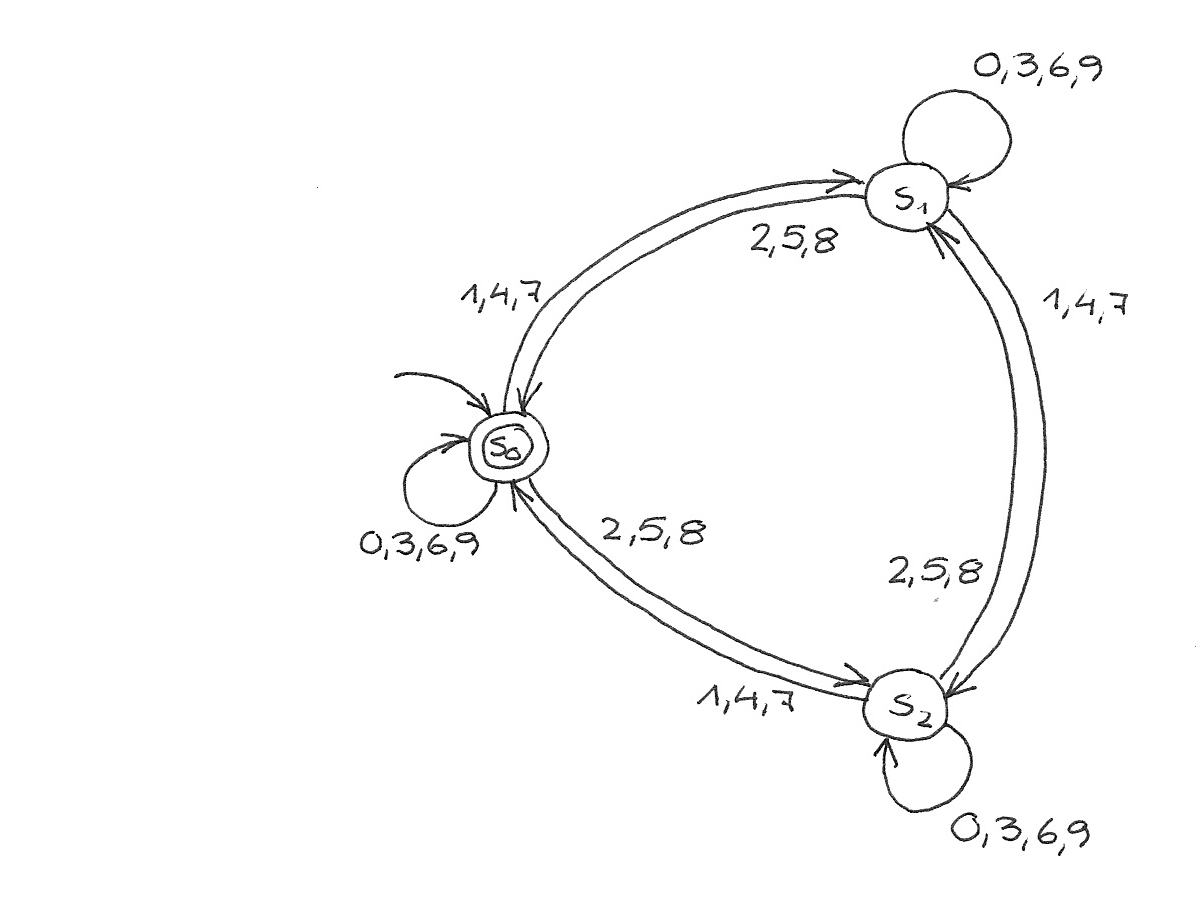
Na, nicht so ganz. Das leere Wort (keine Eingabe) repräsentiert keine Zahl, die irgendwie teilbar wäre. Der Anfangszustand darf nicht Endzustand sein.
Ich will hier niemanden scharf ankucken; bei der ersten Aufgabe (dem 4er) war auch nicht nur einer zunächst in dasselbe offene Messer gerannt.
Beim 4er (wie auch beim 2er im Bild oben) war der Trick, den Pfeil einfach auf einen anderen passenden Zustand zu setzen. Das funktioniert hier aber nicht, weil keiner passt. Wir müssen s₀ in s₀ und sₑ aufdröseln, die ansonsten identisch „verdrahtet“ sind – nur dass einer Endzustand ist und der andere nicht.
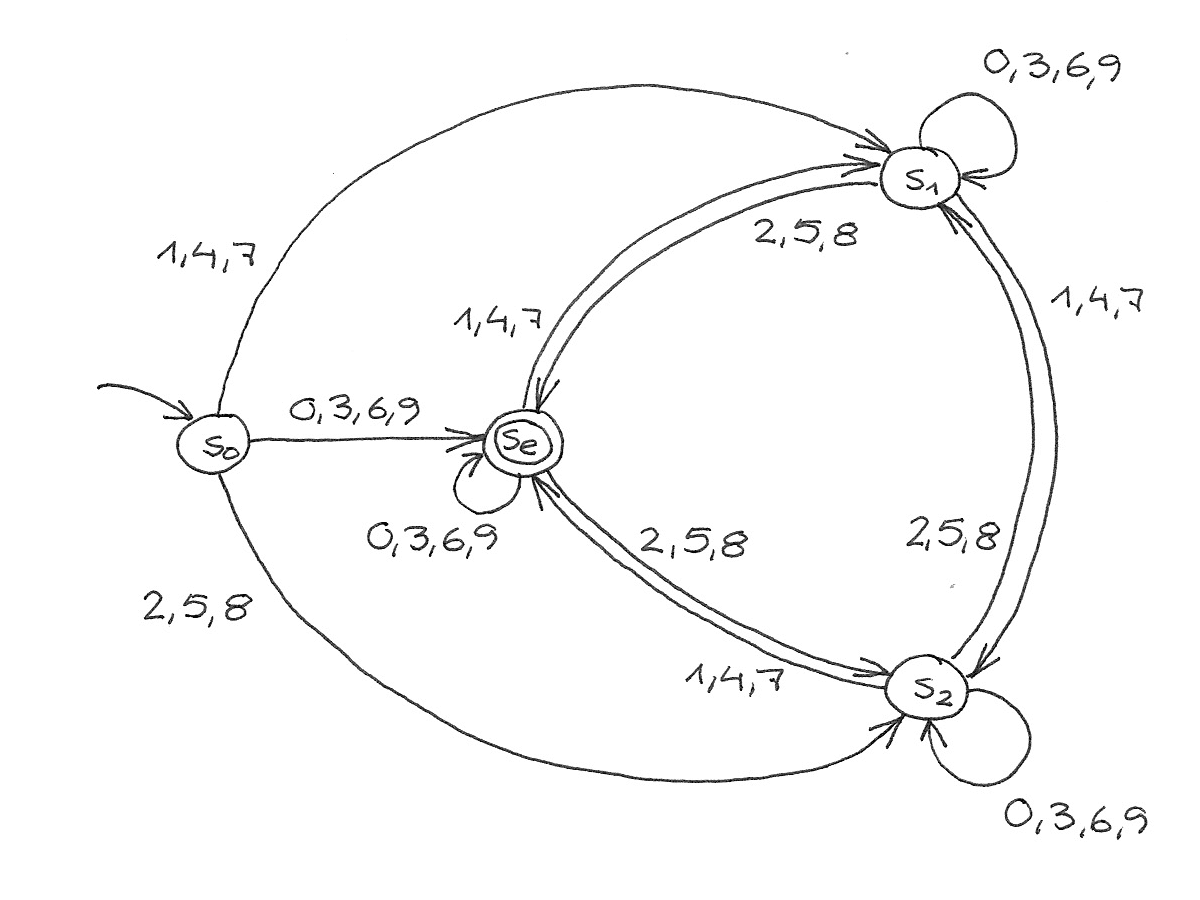
Und wenn man den hat, hat man auch durch geringfügige Modifikation den für 6. Und den für 15.
Teilbarkeit durch 6 heißt Teilbarkeit durch 2 und durch 3. Hier muss man nun nicht Zustände aufdrösen, sondern Übergange, d.h. die Pfeile. Zum Endzustand sₑ führen nur gerade Zahlen als letzte Ziffer (innerer Ring); die ungeraden führen zu einem Zustand, der im Kreis der Teilbarkeit durch 3 eine äquivalente Stelle wie sₑ einnimmt – und einen solchen haben wir schon: das ist ja gerade s₀! (äußerer Ring)
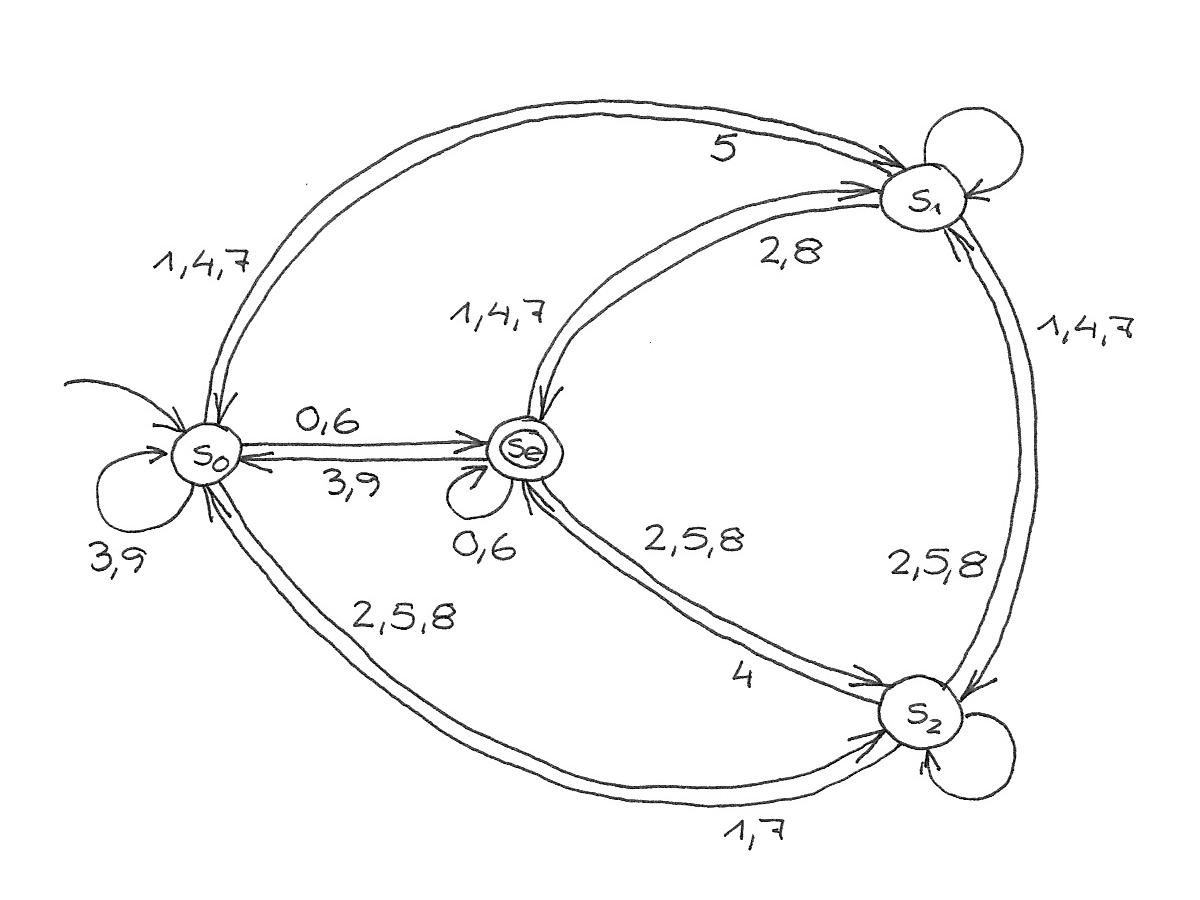
Teilbarkeit durch 15 heißt Teilbarkeit durch 3 und durch 5. Zum Endzustand sₑ führen nur 0 und 5 als letzte Ziffer (innerer Ring); die anderen führen zu s₀ (äußerer Ring):
LLAP 🖖
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann