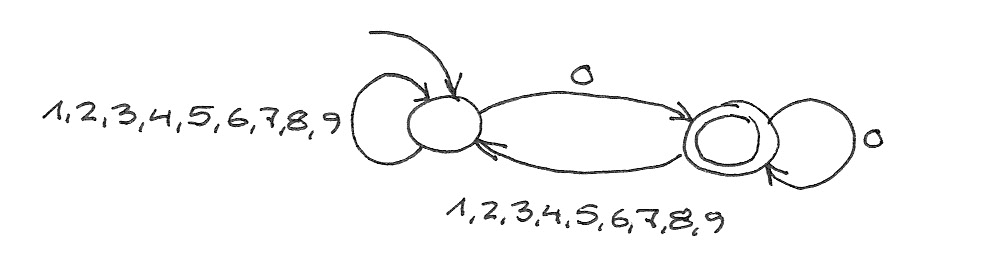@@Gunnar Bittersmann
Hier noch mal alle Automaten aus dem Thread gesammelt. Die Bilder verlinken auf die entsprechenden Postings.
Teilbarkeit durch:
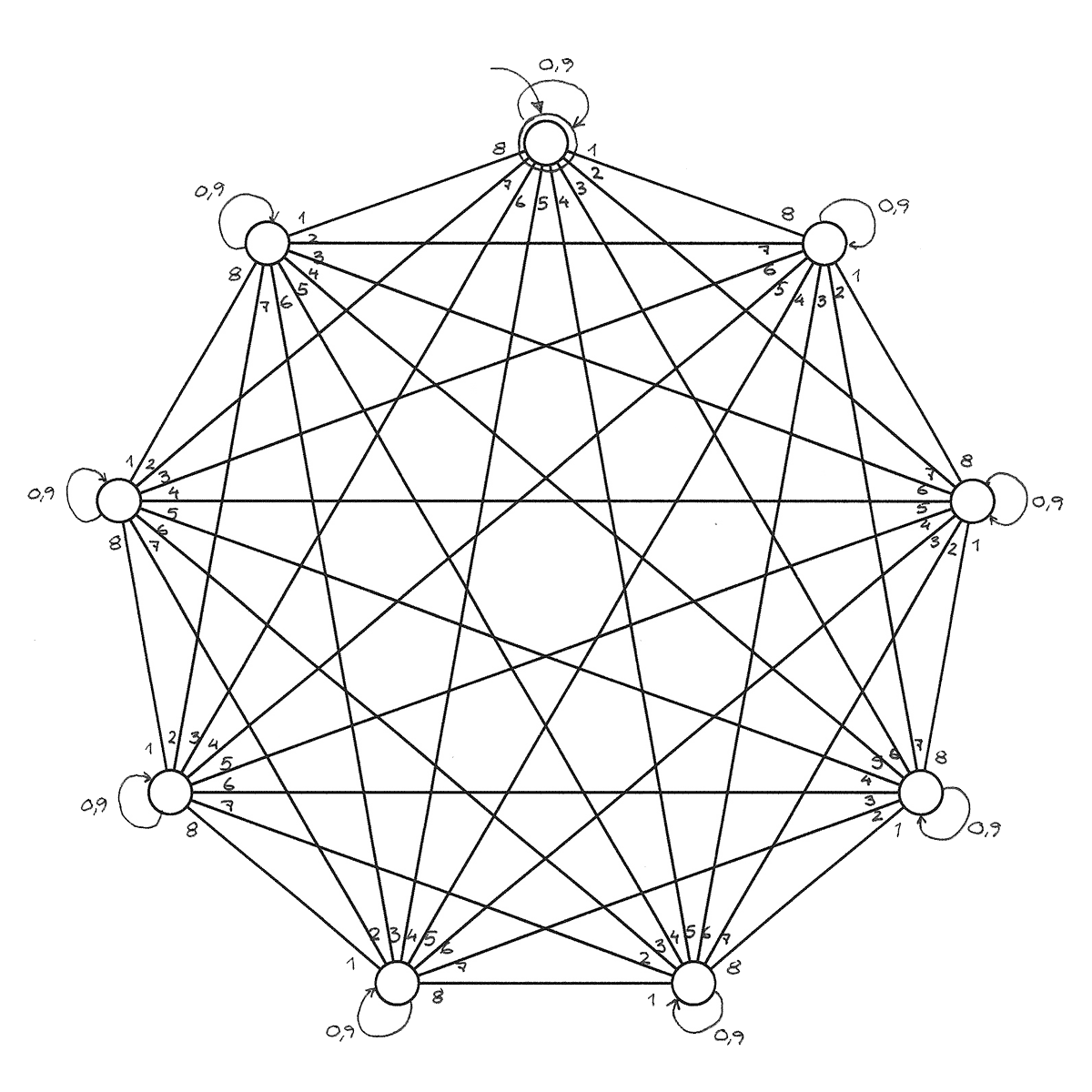
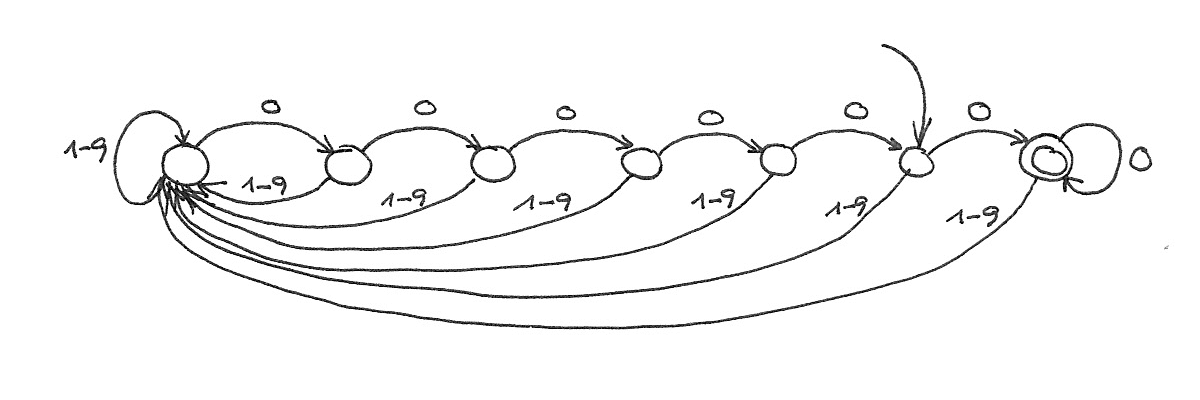 ◀︎ 1000000
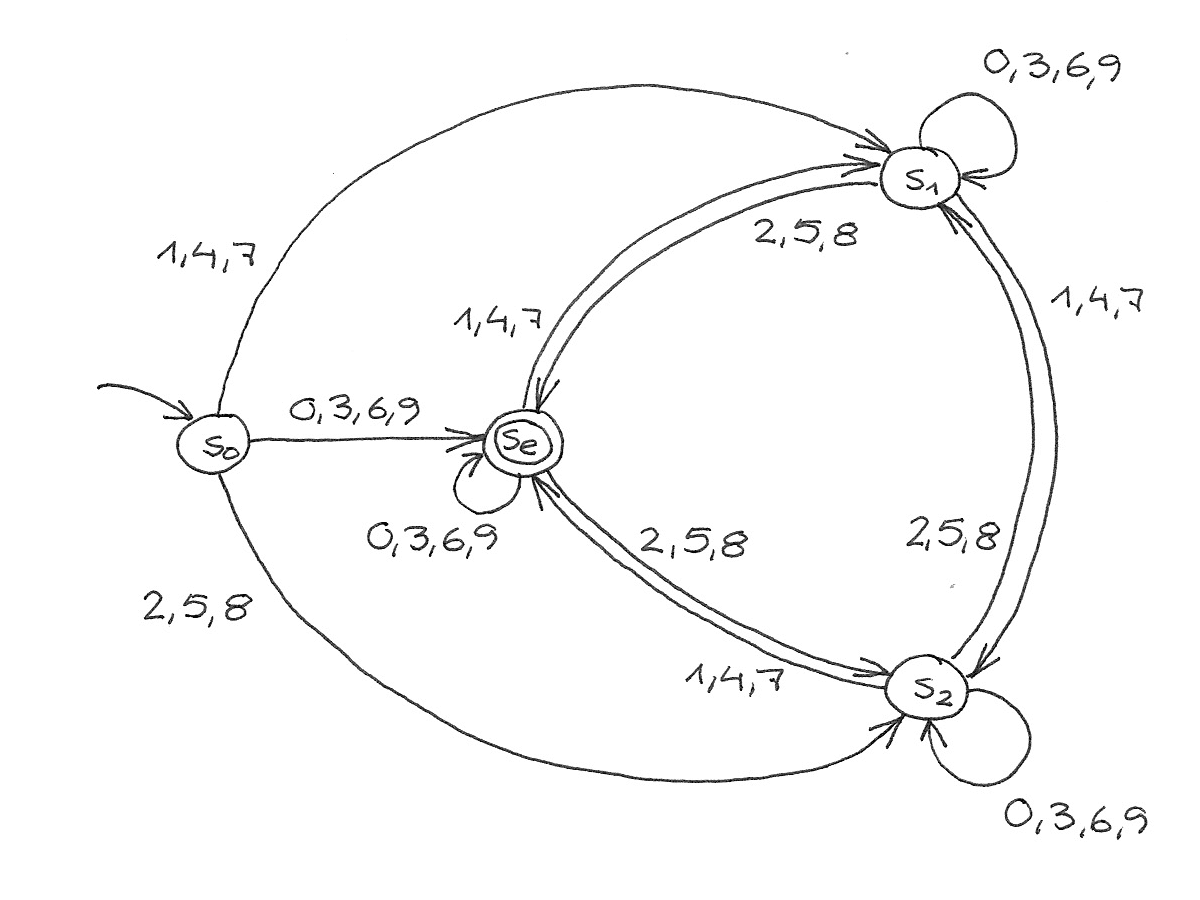
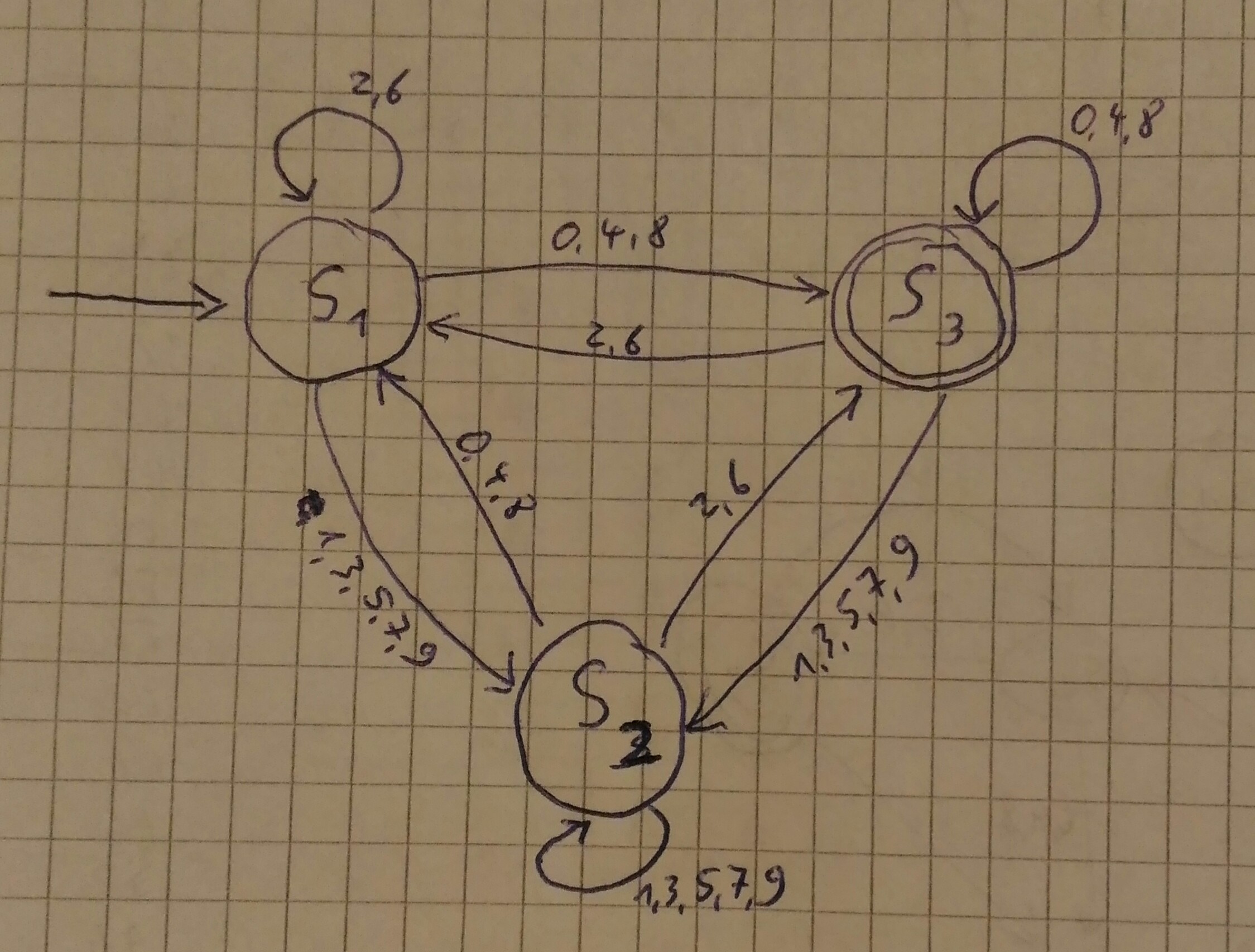
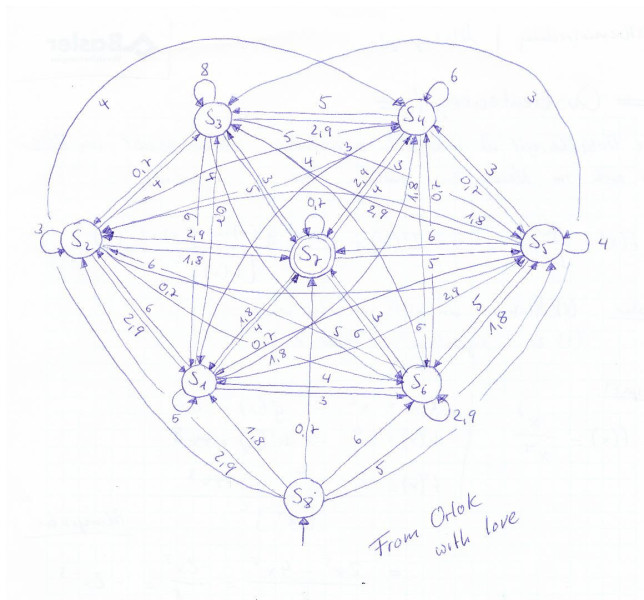
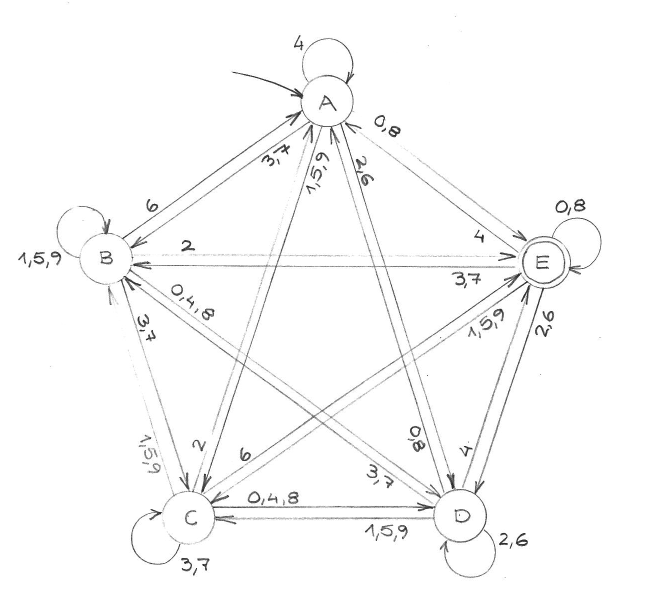
$$\left( {s_{-0}, s_0, \ldots, s_{n-1}}, s_{-0}, {0, \ldots, 9}, \delta(s_u, d) = s_{(10u + d) \bmod n}, {s_0} \right)$$ ◀︎ n
◀︎ 1000000
$$\left( {s_{-0}, s_0, \ldots, s_{n-1}}, s_{-0}, {0, \ldots, 9}, \delta(s_u, d) = s_{(10u + d) \bmod n}, {s_0} \right)$$ ◀︎ n
ohne führende 0:
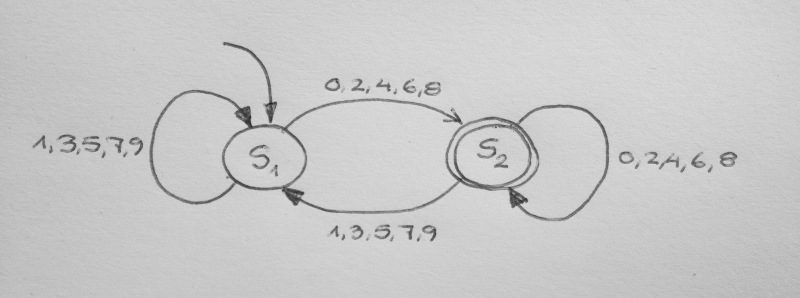
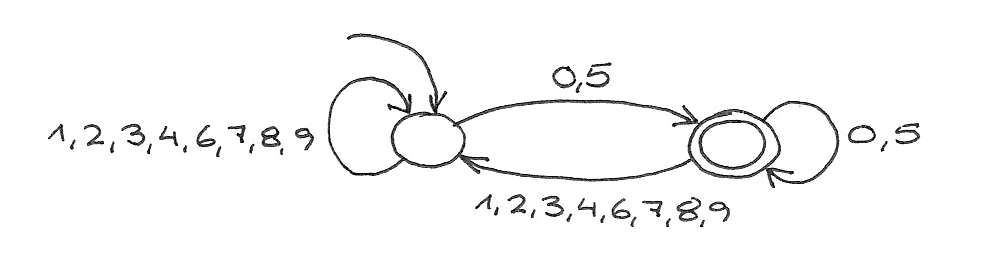
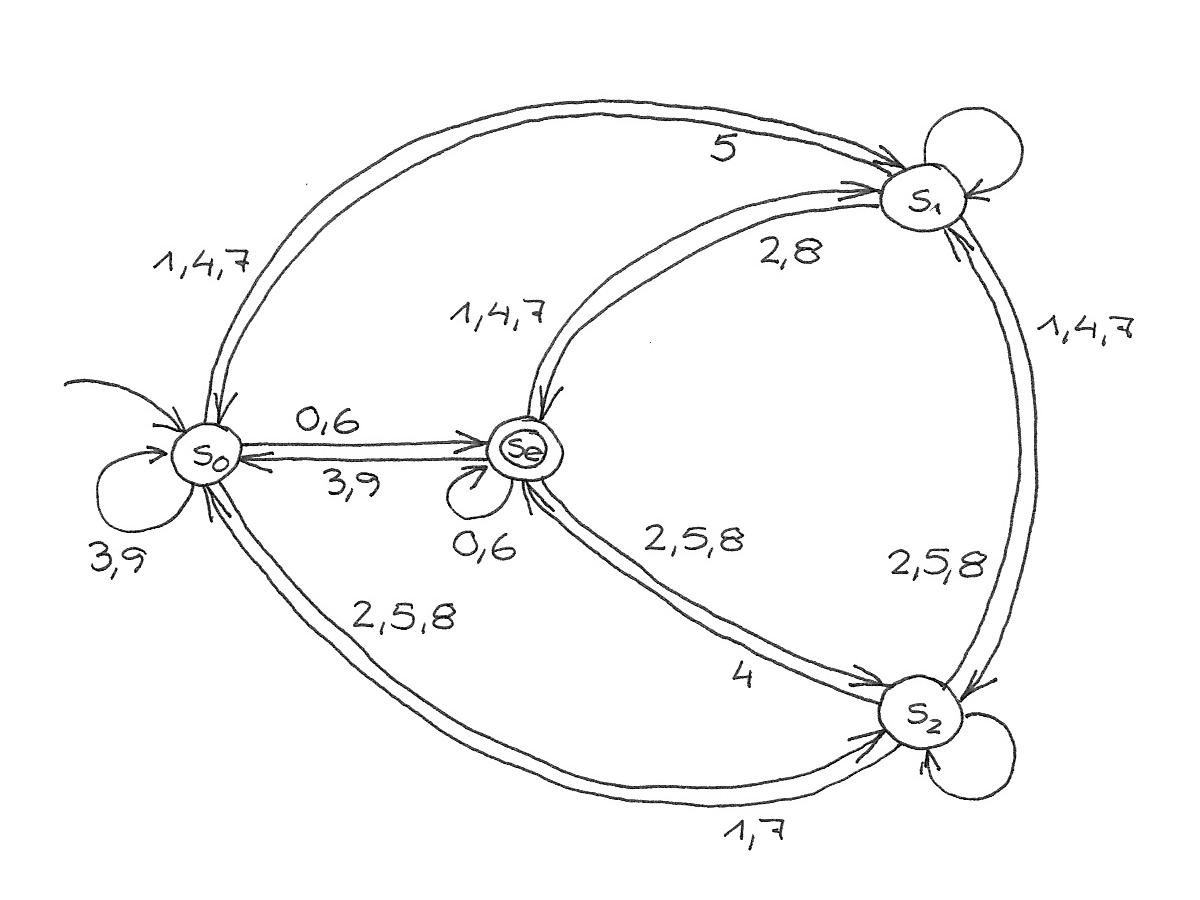
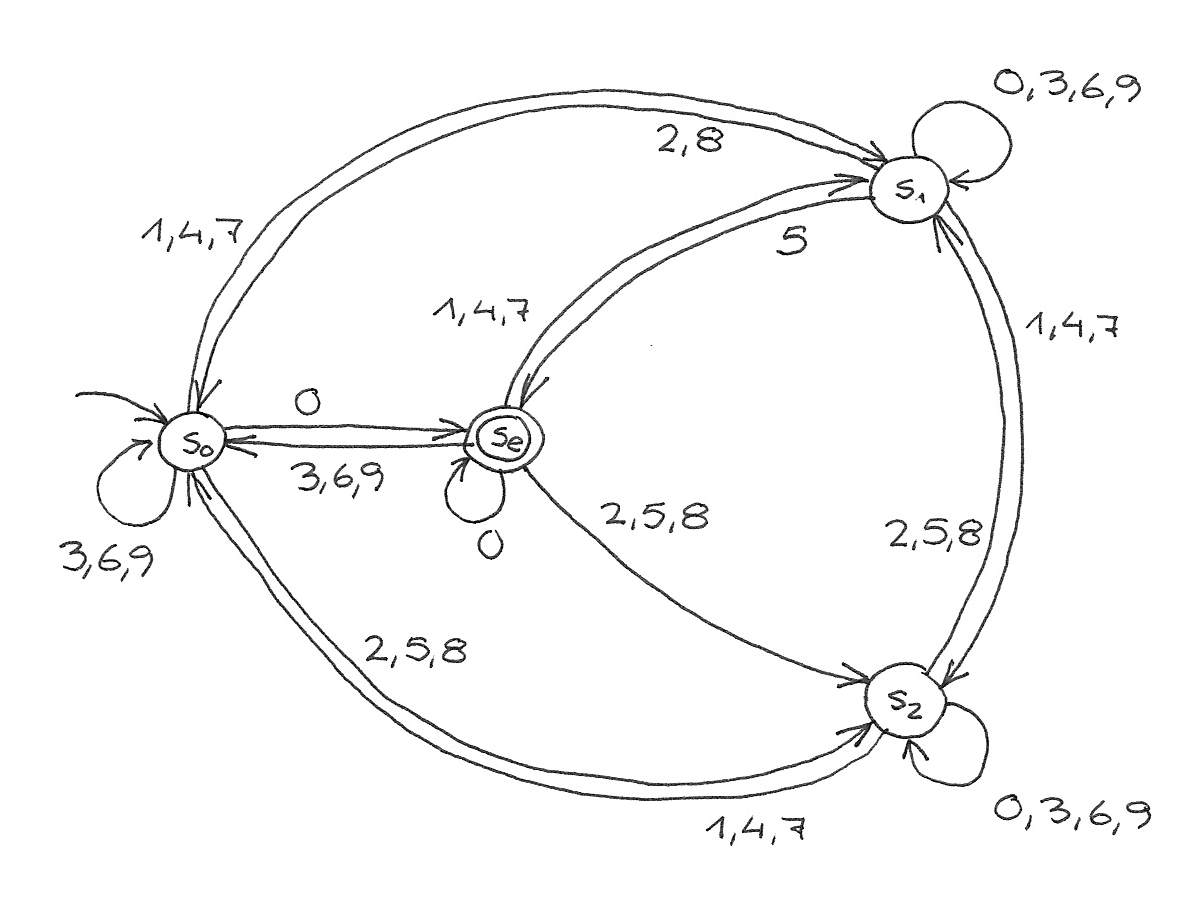
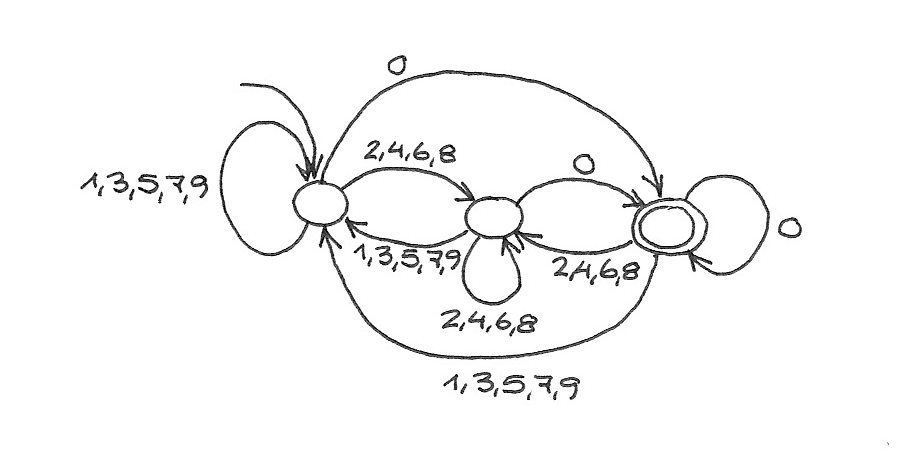
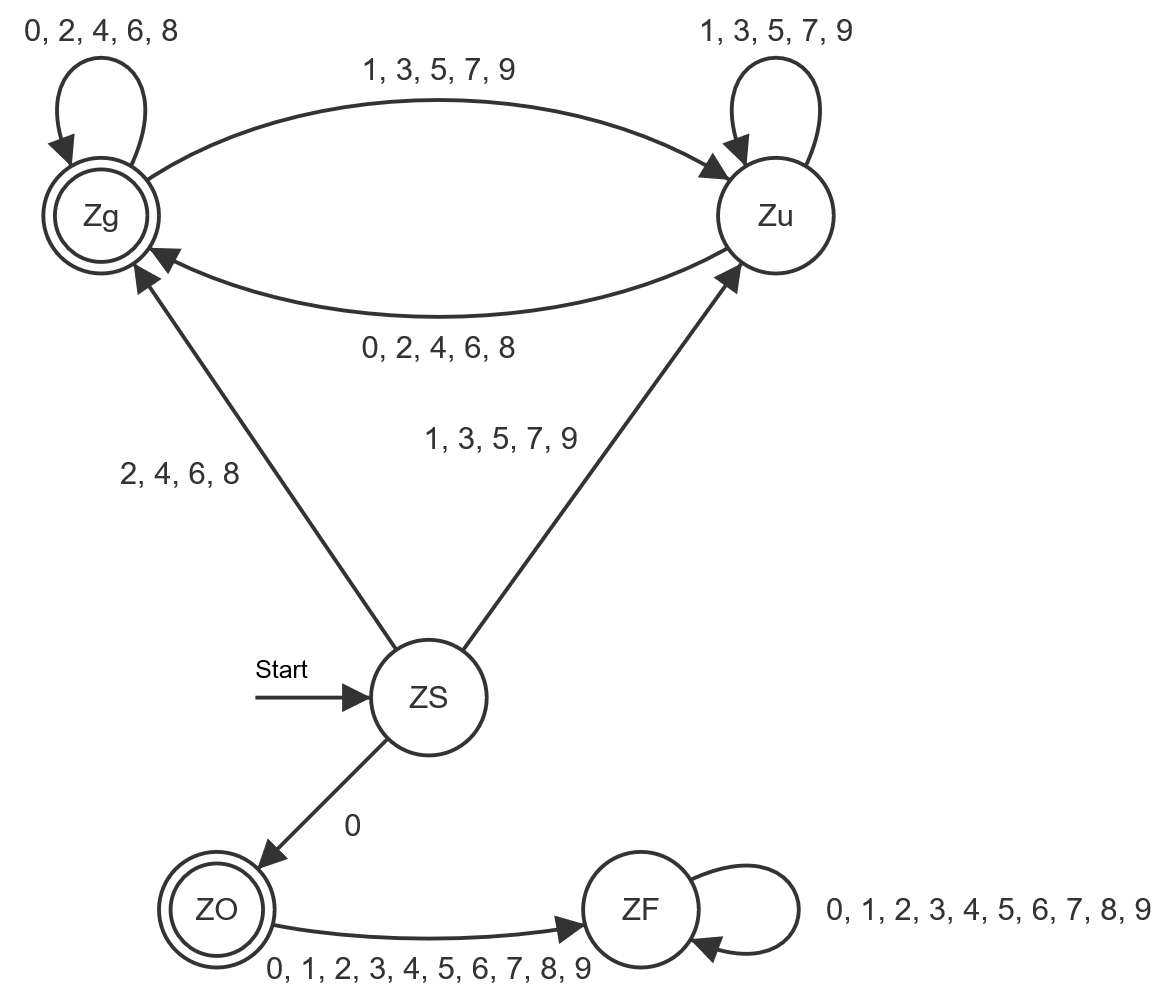 ◀︎ 2
$$\delta(s_u, d) = \begin{cases}
s_{v = (10u + d) \bmod n}
◀︎ 2
$$\delta(s_u, d) = \begin{cases}
s_{v = (10u + d) \bmod n}
s_{\mathrm{zero}}
s_{\mathrm{trap}}
\end{cases}$$ ◀︎ n
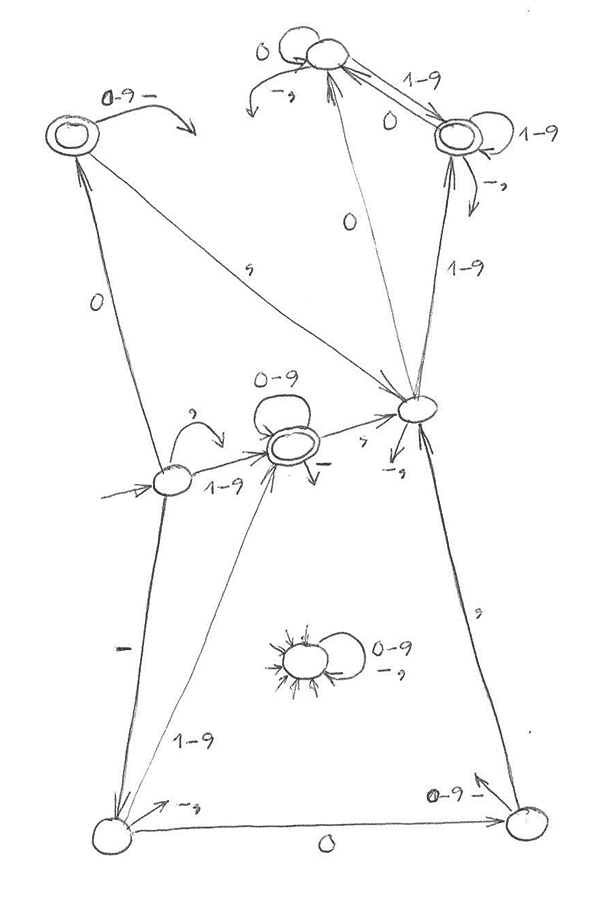 ◀︎ Dezimalzahl
◀︎ Dezimalzahl
LLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann