Informatik zum Jahresanfang – noch eine Variation

[Gunnar Bittersmann]

@@Matthias Apsel

Hallo Gunnar Bittersmann,

Hier sieht man auch schön, wann sich ein Automat nicht reduzieren lässt:

es gilt also δ(α, σ) = δ(β, σ) für alle Symbole σ ∈ Σ.

Dennoch kann man die Zustände α und β nicht zu einem zusammenfassen, weil α ein Endzustand ist, β aber nicht.

Der Automat könnte sich aber trotzdem reduzieren lassen. Schließlich hat er noch andere Zustände.

Zum Beispiel γ rechts oben (nennen wir ihn „Bellatrix“) und den Kopf λ (nennen wir ihn „Heka“): Von beiden geht’s mit 0 zu λ und mit 1 bis 9 zu γ sowie mit − und , in den Nebel. Keine Reduktion, obwohl δ(γ, σ) = δ(λ, σ) für alle Symbole σ ∈ Σ, weil γ ein Endzustand ist, λ aber nicht.

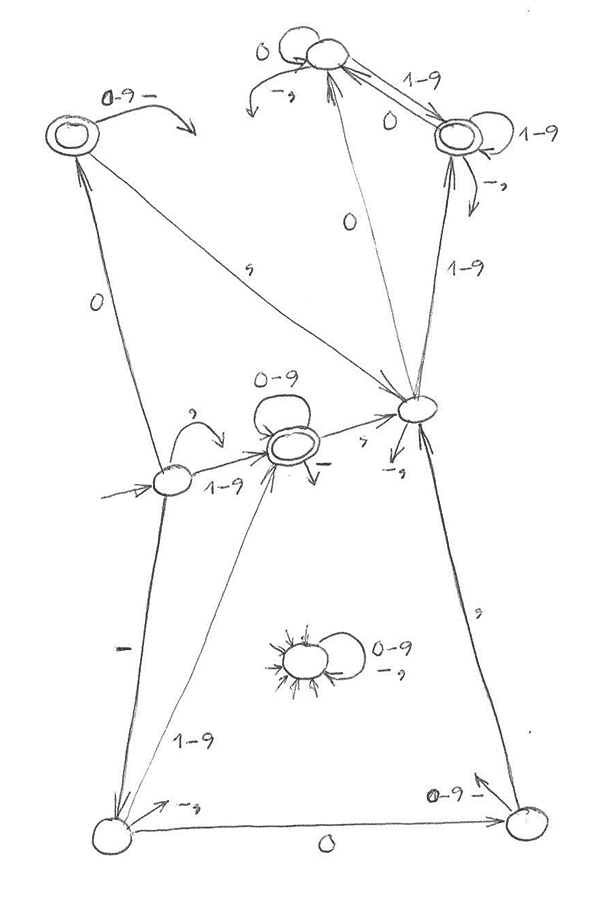
Anders siehts aus, wenn man bei Dezimalbrüchen Nullen am Ende zulässt. (Was ja in der Physik durchaus Sinn macht: 9876,50 ist was anderes als 9876,5 – nämlich eine genauere Messung/Berechnung aus genaueren Messwerten.)

Dann ist λ auch ein Endzustand; γ und λ können zusammengefasst werden. Dazu werden die zu γ führenden Pfeile (von γ selbst und vom rechten Gürtelzustand δ) mit 0–9 beschriftet; λ und alle Pfeile von und zu diesem werden entfernt.

LLAP 🖖