Informatik zum Jahresanfang – noch eine Variation

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Ich mach mal den Columbo: Eine Frage hätte ich da noch. Wie müsste man den Automaten verändern, wenn führende Nullen nicht erlaubt sind?

Wie „ein Sektglas. Passend zum Jahresanfang.“ —@Matthias Apsel

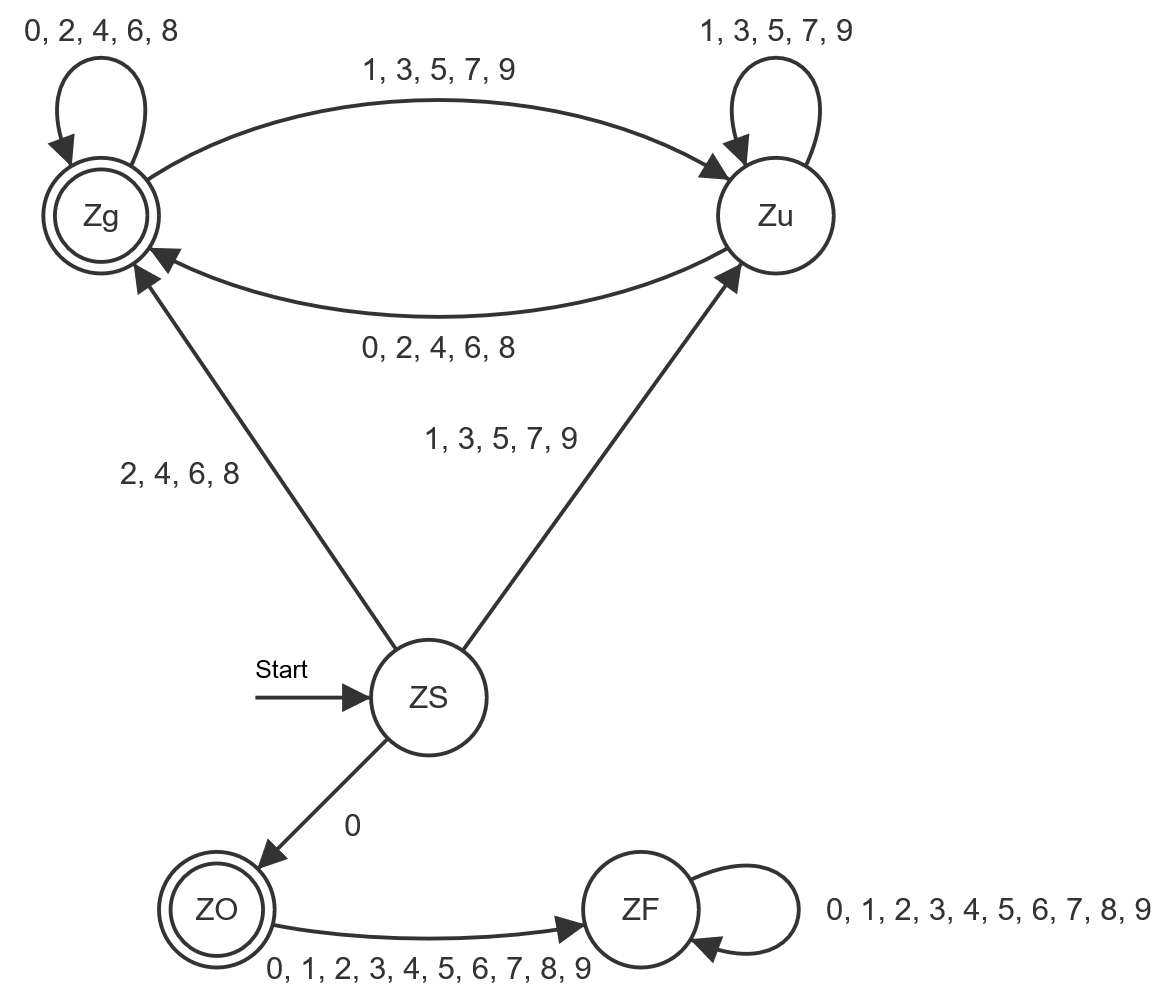
Das lässt sich auch verallgemeinern: Wir brauchen in dem allgemeinen Automaten für n zwei zusätzliche Zustände; ich nenne sie mal $$s_{\mathrm{zero}}$$ und $$s_{\mathrm{trap}}$$ (entsprechen ZO und ZF im Fuß von Matthias’ Sektglas), wobei $$s_{\mathrm{zero}}$$ ein weiterer Endzustand ist. Dann ist also

$$\begin{align} S &= {s_{-0}, s_{\mathrm{zero}}, s_{\mathrm{trap}}, s_0, s_1, \ldots, s_n}
F &= {s_{\mathrm{zero}}, s_0} \end{align}$$

(wobei der Startzustand $$s_{-0}$$ dem ZS in Matthias’ Sektglas entspricht).

In der Übergangsfunktion müssen wir den Pfeil für die 0 von $$s_{-0}$$ zu $$s_{\mathrm{zero}}$$ umbiegen (ZS → ZO) und die Ausgänge von $$s_{\mathrm{zero}}$$ und $$s_{\mathrm{trap}}$$ zu $$s_{\mathrm{trap}}$$ (→ ZF) hinzufügen:

$$\delta(s_u, d) = \begin{cases} s_v \text{ mit } v = (10u + d) \bmod n & \text{ für } u = 0, \ldots, 9\text{ sowie für } u = -0 \text{ und } d = 1, \ldots, 9
s_{\mathrm{zero}} & \text{ für } u = -0 \text{ und } d = 0
s_{\mathrm{trap}} & \text{ für } s_u \in {s_{\mathrm{zero}}, s_{\mathrm{trap}}} \end{cases}$$

LLAP 🖖