Mathematik zur Wochenmitte - Lösung

[Gunnar Bittersmann]

@@ottogal

Nur Gunnar hat eine Lösung mitgeteilt, mit einer anderen Herleitung der Kongruenz der beiden Dreiecke.
@Gunnar Bittersmann : Magst du sie hier zeigen?

Ja, gerne. Wo ich doch schon die Skizze hier gespoilert hatte …

Meine Lösung ist ein Zweiteiler. Der erste:

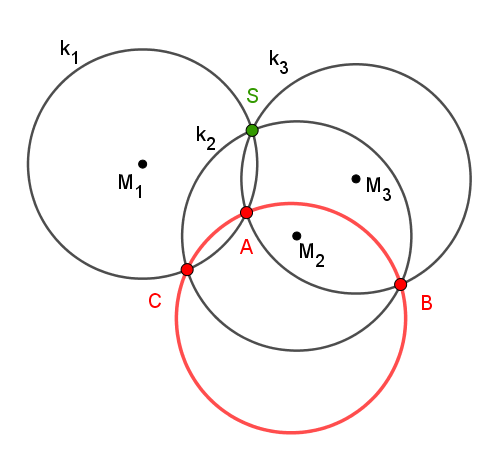
Da S auf k₁, k₂ und k₃ liegt, ist M₁S = M₂S = M₃S = r. S ist also der Mittelpunkt des Umkreises des Dreiecks M₁M₂M₃; dessen Radius ist r.

Wie man leicht sieht, sind die Dreiecke M₁M₂M₃ und ABC kongruent. Folglich hat auch der Umkreis des Dreiecks ABC den Radius r, q.e.d.

Garstigerweise ließ @ottogal „Wie man leicht sieht“ nicht gelten und meinte, ich „möchte dies noch ein wenig sehen machen“.

Ertappt. 🤭 Ich hatte zu dem Zeitpunkt noch keinen blassen Schimmer.

Teil 2: Irgendwann kam dann das Ηὕρηκα! und ich hab’s gesehen:

Die Gleichheit der Größen der mit α, α′, β, β′, γ und γ′ bezeichneten Winkel ergibt sich daraus, dass AS, BS und CS die Mittelsenkrechten zu M₁M₃, M₂M₃ und M₁M₂ sind.

Wegen Winkelsummen: α′ = 90° − α, β′ = 90° − β, γ′ = 90° − γ. Aus 2α′ + 2β′ + 2γ′ = 360° folgt α′ = β + γ, β′ = α + γ, γ′ = α + β.

Damit ist ∠M₃AM₁ = ∠CM₂B. Außerdem stimmen die Dreiecke M₃M₁A und CBM₂ in den Schenkeln AM₁ = AM₃ = M₂B = M₂C = r überein, sind also nach SWS kongruent. Folglich M₁M₃ = BC.

Analog zeigt man M₂M₃ = AC und M₁M₂ = AB. Damit sind die Dreiecke M₁M₂M₃ und ABC nach SSS kongruent.

Und wie so oft ist ottogals Lösung die einfachere, elegantere.

🖖 Stay hard! Stay hungry! Stay alive! Stay home!