Mathematik zur Abkühlung – Lösung

[Matthias Apsel]

Hallo Matthias Apsel,

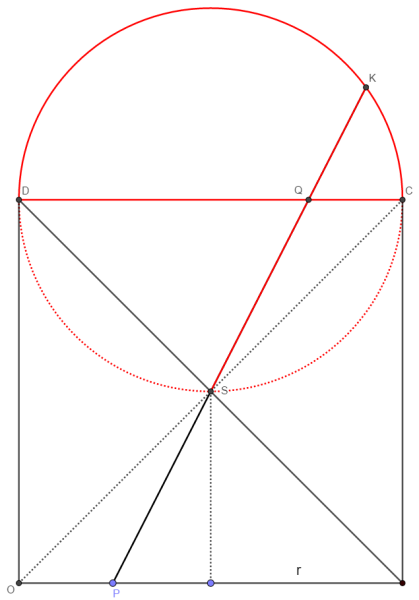
wie so oft, ist die Wahl der richtigen Hilfslinie wichtig. Diesmal ist es die andere Hälfte des Kreises.

Um Brüche im Nenner zu vermeiden, nehmen wir nicht die Seitenlänge des Quadrates, sondern den Radius des Kreises als Parameter. Die Länge der Strecke OP sei p.

DC und SK sind Sehnen desselben Kreises. Für die gilt der Sehnensatz, den @ottogal auch verwendet hat, allerdings ohne ihn zu nennen, dafür fällt bei ihm der Beweis quasi nebenbei mit ab.

Sehnensatz: Das Produkt der Sehnenabschnitte der einen Sehne ist gleich dem Produkt der Sehnenabschnitte der anderen Sehne.

Damit gilt:

DQ = 2r - p
QC = p

SQ = PS

PS lässt sich über den Pythagoras ermitteln: $$\overline{PS}^2=r^2+(r-p)^2$$, für QK kann der Sehnensatz verwendet werden.

$$QK = \frac{(2r-p) \cdot p}{\sqrt{r^2 + (r-p)^2}}$$

Damit ist Teil b) erledigt.

Für Teil a) können wir noch ein bisschen addieren und erhalten:

$$SK = \frac{2r}{\sqrt{r^2 + (r-p)^2}}$$

Mit r = 12 und p = 3 ergibt sich SK = 96/5.

Alternativ kann man auch hier den Sehnensatz verwenden. Das Dreieck zur Berechnung von PS hat die Katheten 9 und 12, also ist PS = SQ = 15 (3-4-5-Dreieck). Die beiden anderen Sehnenabschnitte sind 3 und 21.

Damit ist die gesuchte Streckenlänge $$15 + \frac{3 \cdot 21}{15}$$

Bis demnächst
Matthias