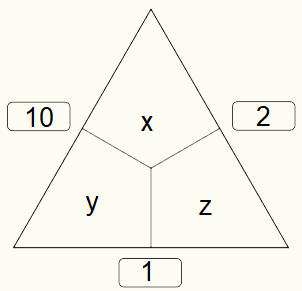
Hallo Friedel,
erst Teil c verlangt, ein Kriterium zu finden, dass alle inneren Zahlen natürlich und positiv sind.
Ohne diese Forderung ist es zur Lösbarkeit auch gültig, innen z.B. ein $$-\frac{1}{2}$$ hinzuschreiben. Zumindest habe ich das so verstanden. Die folgende Aufgabe ist lösbar.
x = 5,5 / y = 4,5 / z = -3,5
Natürlich löst das kein Primarstufenschüler. Für diese braucht es - meine ich - zwei Kriterien (oder 4, je nach Zählweise), um eine primarfreundliche Aufgabe zu erhalten.
Aber damit hast Du mir nun ein <i> verkauft 😲
Natürlich sieht man sofort, dass die Aufgabe nicht primar-lösbar ist, wenn außen irgenwo eine 1 steht. Wenn x, y natürlich und positiv sein sollen, ist x+y mindestens 2. Aber die Kriterien, die ich eingeschickt habe, sehen anders aus. Meine Herausforderung ist jetzt, unter Anwendung dieser Kriterien zu zeigen, dass dann eine Lösung nicht möglich ist 🤔.
Edit: Ah, puh, geschafft.
Rolf
sumpsi - posui - obstruxi