Mathematik zum Wochenende – Lösung der Zusatzaufgabe

[Gunnar Bittersmann]

@@Rolf B

Mich würden aber noch die einzelnen Flächenanteile der vier weißen Flächen interessieren!

Hier setzen wir nun aber doch o.B.d.A. r = 1. Die Fläche des großen Viertelkreises ist dann ⁵⁄₄π; die des kleinen Dreiviertelkreises ¾π (siehe Lösung).

Die Fläche links unten beträgt 1 − ¼π; deren Anteil also $$\frac{1 - \frac{1}{4} \pi}{\frac{5}{4} \pi} = \frac{4 - \pi}{5 \pi} = \frac{\frac{4}{\pi} - 1}{5} \approx 0.055$$

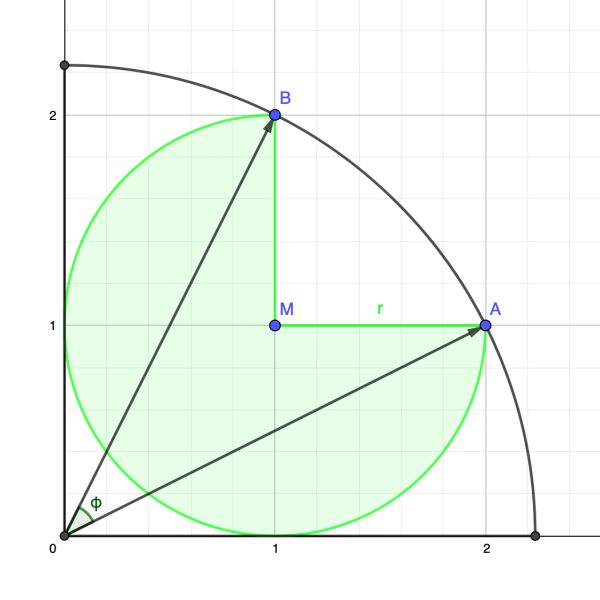
A(2, 1), B(1, 2), M(1, 1)

Für die Fläche rechts oben brauchen wir den Winkel φ des Kreissektors OAB. Den holen wir uns über das Skalarprodukt der Vektoren a⃗ = OA und b⃗ = OB:

$$\cos \phi = \frac{\vec a \cdot \vec b}{|\vec a| |\vec b|} = \frac{\tbinom{2}{1} \cdot \tbinom{1}{2}}{R^2} = \frac{4}{5}$$, also φ = arccos ⅘.

(Das dürfte einfacher sein als von rechten Winkel zweimal den Winkel im Dreieck abzuziehen, d.h. φ = ½π − 2 arctan ½.)

(Und auch hier taucht R² auf; also nirgendwo eine Wurzel.)

Von der Fläche des Kreissektors OAB müssen wir noch die des Vierecks OAMB abziehen. Die Diagonale OM teilt dieses in zwei Dreiecke der Grundseite 1 und Höhe 1; Flächeninhalt von OAMB ist also 1.

Das ergibt für die Fläche rechts oben φ/2π · 5π − 1; der Anteil ist also $$\frac{\frac{5}{2} \phi - 1}{\frac{5}{4} \pi} = \frac{10 \phi - 4}{5 \pi} \approx 0.155$$.

Die Flächen links oben und rechts unten teilen sich den Rest der weißen Fläche (die ja ⅖ des Viertelkreises ist) abzüglich der Flächen links unten und rechts oben. Deren Anteil ist also jeweils

$$\frac{1}{2} \left( \frac{2\pi}{5\pi} - \frac{4-\pi}{5\pi} - \frac{10\phi-4}{5\pi} \right) = \frac{1}{2} \left( \frac{3\pi-10\phi}{5\pi} \right) = \frac{3}{10} - \frac{\phi}{\pi} \approx 0.095$$.

Wenn ich mich nicht verrechnet habe.

😷 LLAP