nicht angemeldet
Mathematik zur Wochenmitte
Gunnar Bittersmann
Mathematik zur Wochenmitte
Gunnar Bittersmann
MudGuard
Rolf B
Der MartinWie letzte Woche werden wir wohl auch hier wieder (nicht) integrieren müssen. 😉
Das Quadrat hat die Fläche 36. Wie groß ist die grün ausgemalte Fläche des rechtwinkligen Dreiecks?
Lösungen wie immer bitte nicht hier posten, sondern per DM (Post) an mich. Ich löse dann in ein paar Tagen auf.
😷 LLAP
--
„Dann ist ja auch schrecklich, dass wir in einem Land leben, in dem nicht nur Bildungswillige leben, sondern auch hinreichende Zahlen von Bekloppten. Das darf ich so locker formulieren, ich bin ja jetzt Rentner und muss nicht mehr auf jedes Wort achten.“
— Joachim Gauck über Impfgegner
„Dann ist ja auch schrecklich, dass wir in einem Land leben, in dem nicht nur Bildungswillige leben, sondern auch hinreichende Zahlen von Bekloppten. Das darf ich so locker formulieren, ich bin ja jetzt Rentner und muss nicht mehr auf jedes Wort achten.“
— Joachim Gauck über Impfgegner
-
Hi,
Wie letzte Woche werden wir wohl auch hier wieder (nicht) integrieren müssen. 😉
Das Quadrat hat die Fläche 36. Wie groß ist die grün ausgemalte Fläche des rechtwinkligen Dreiecks?
Der Punkt unten ist in der Mitte der Quadratseite?
cu,
Andreas a/k/a MudGuard-
@@MudGuard
Der Punkt unten ist in der Mitte der Quadratseite?
Ja. Die Kennzeichnung ⧺ zeigt an, dass die beiden so markierten Strecken gleich lang sind.
😷 LLAP
--
„Dann ist ja auch schrecklich, dass wir in einem Land leben, in dem nicht nur Bildungswillige leben, sondern auch hinreichende Zahlen von Bekloppten. Das darf ich so locker formulieren, ich bin ja jetzt Rentner und muss nicht mehr auf jedes Wort achten.“
— Joachim Gauck über Impfgegner
-
-
@@Gunnar Bittersmann
Die Aufgabe stammte mal wieder von Catriona Agg.
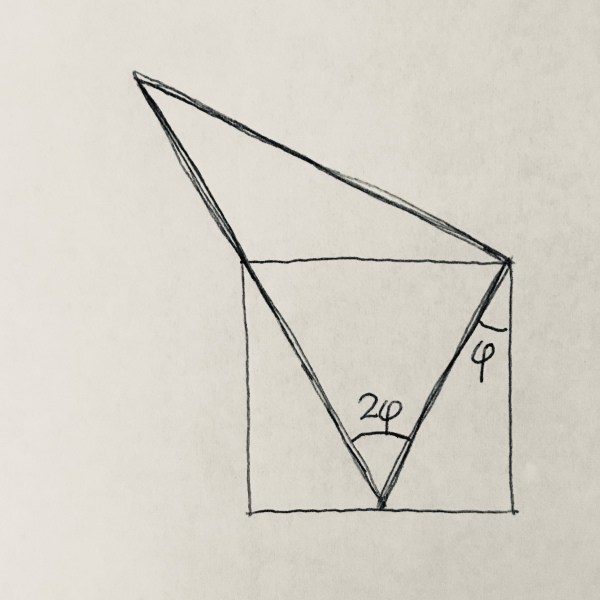
Wir legen das Quadrat in ein Koordinatensystem – am einfachsten wird die Rechnung wohl so, wie es @MudGuard gelegt hat: mit dem linken oberen Eckpunkt in den Koordinatenurprung O. Der rechte obere Eckpunkt sei A; der Mittelpunkt der unteren Seite M.
Die Gerade OM hat die Gleichung y = −2x. Die Gerade AM hat den Anstieg 2; die Senkrechte dazu also den Anstieg −½ und damit sie durch den Punkt A(6, 0) geht, ist es y = −½x + 3. Ihr Schnittpunkt P mit OM ergibt sich aus −2x = −½x + 3 zu P(−2, 4).
@MudGuard hatte die gesuchte Fläche aufgeteilt: MAP = OPA + OMA = ½ · 6 · 4 + ½ · 6 · 6 = 30. 👴👵
Das ist noch einfacher, als es @Rolf B und ich gemacht hatten: die Kathetenlängen von △MAP zu AM = √(6² + 3²) = 3√5 und AP = √(8² + 4²) = 4√5 bestimt. ½ · 3√5 · 4√5 = 30.
Eine andere Möglichkeit, völlig ohne Koordinatensystem und Geradengleichungen an die längere Kathete zu kommen (die kürzere ist ja einfacher Pythagoras), ergibt sich aus dem Tangens und dessen Doppelwinkelfunktion tan 2φ = 2 tan φ / (1 − tan² φ).
Für tan φ = ½ ist tan 2φ = ⁴⁄₃. AP = AM · tan 2φ = 3√5 · ⁴⁄₃ = 4√5. (@RonySarker71)
Eine ganz andere Lösung ergibt sich über eine geometrische Reihe. @Tabellenkalk schrieb:
Wir haben also ein Quadrat, bestehend aus vier identischen Dreiecken und darauf einen Zipfel, der etwas größer als ein solch Dreieck ist. Also etwas größer als ein Viertel.
Denn dieses Dreieck hat wieder so einen Zipfel etwas größer als ein Viertel, und so weiter...Also ein Viertel plus davon ein Viertel plus davon...
Das konvergiert gegen 4/3.
Also 36 × 4 ÷ 3 = 48
Angefangen haben wir aber nur mit der Hälfte des Quadrats, also 18 abziehen: A = 30.
Auch @Rolf B und @dare2solve kamen auf diese Lösung.
Es geht aber auch ohne „höhere Mathematik“: einfach mit Strahlensatz, wie @ottogal zeigte:
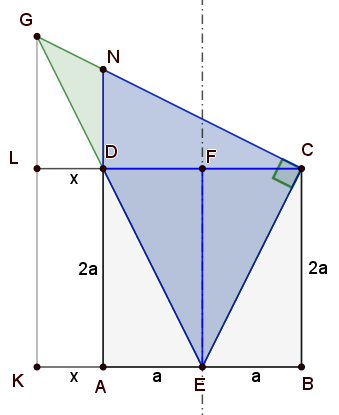
Sei $$N$$ der Schnittpunkt der Geraden $$AD$$ und $$GC$$.
Die drei blauen Dreiecke sind zueinander kongruent, da sie in den Winkeln und in einer Kathete übereinstimmen. Daraus folgt $$|ND|=a$$.
Wie vorher sei $$|LD|=x$$, und wegen der Ähnlichkeit von $$ \triangle LDG$$ und $$ \triangle AED$$ ist $$|GL|=2x$$.
Nun sind auch $$ \triangle LCG$$ und $$ \triangle DCN$$ wegen übereinstimmender Winkel ähnlich. Daher gilt
$$\frac{|GL|}{|ND|} = \frac{|LC|}{|DC|}$$,
also $$\frac{2x}{a} = \frac{x+2a}{2a}$$.
Es folgt $$4x = x+2a$$ und somit $$x=\frac{2}{3} a$$.
Die Fläche von $$\triangle DCG$$ berechnet sich damit zu $$\frac{1}{2} |DC| \cdot |GL| = \frac{1}{2} \cdot 2a \cdot 2x = 2ax = \frac{4}{3}a^2$$.
$$\triangle DEC$$ hat natürlich die Fläche $$2a^2$$.
Addiert erhält man die gesuchte grüne Fläche zu $$\frac{10}{3}a^2$$.
Die Vorgabe $$4a^2=36$$ heißt $$a=3$$, somit ist das Ergebnis $$30$$.
😷 LLAP
--
„Dann ist ja auch schrecklich, dass wir in einem Land leben, in dem nicht nur Bildungswillige leben, sondern auch hinreichende Zahlen von Bekloppten. Das darf ich so locker formulieren, ich bin ja jetzt Rentner und muss nicht mehr auf jedes Wort achten.“
— Joachim Gauck über Impfgegner-
Hallo Gunnar,
ein +1 an Mudguard für OPA + OMA 😂
Rolf
--
sumpsi - posui - obstruxi-
@@Rolf B
ein +1 an Mudguard für OPA + OMA 😂
Die Benamsung stammte von mir, aber MudGuard soll der Punkt gegönnt sein.
😷 LLAP
--
„Dann ist ja auch schrecklich, dass wir in einem Land leben, in dem nicht nur Bildungswillige leben, sondern auch hinreichende Zahlen von Bekloppten. Das darf ich so locker formulieren, ich bin ja jetzt Rentner und muss nicht mehr auf jedes Wort achten.“
— Joachim Gauck über Impfgegner -
Hi,
ein +1 an Mudguard für OPA + OMA 😂
ne, das OPA und OMA stammt nicht von mir, ich hatte die Punkte gar nicht mit Buchstaben versehen, sondern von "Quadrat-Unterseite Mitte" und "rechter oberer Eckpunkt" (oder so ähnlich) geschrieben
cu,
Andreas a/k/a MudGuard
-
-
Hallo miteinander,
Die Aufgabe stammte mal wieder von Catriona Agg.
na klar, von wem auch sonst?
@MudGuard hatte die gesuchte Fläche aufgeteilt: MAP = OPA + OMA = ½ · 6 · 4 + ½ · 6 · 6 = 30. 👴👵
Das war auch mein Ansatz. Und mein Bauchgefühl suggerierte mir, dass die Strecken OM und OP gleich lang sein müssten, die Dreiecke OMA und OPA damit flächengleich. Mit fehlte nur ein Ansatz, das auch zu beweisen.
Jetzt weiß ich warum: Weil mein Bauchgefühl einfach falsch war. 😉
Möge der Kaffee gut und der Montag kurz sein
Martin--
The taste of love: The more you get, the more you want
(aus The Lightning Seeds: Sense)
-
