Hallo in die Runde,
ich habe mir inzwischen doch etwas Zeit genommen und versucht, die fragliche Funktion zu ermitteln - wenigstens für einen Fall.
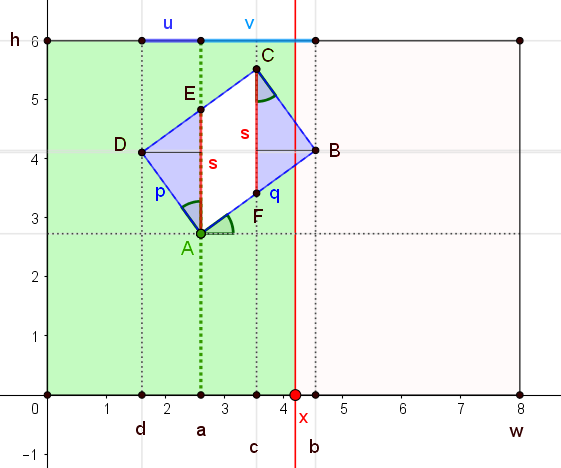
Gegeben sind:
- die Seitenlängen des großen Rechtecks: $$w$$ und $$h$$
- die des ausgeschnittenen Rechtecks ABCD:
$$p=AD=BC$$ und $$q=AB=DC$$ - der Winkel $$\alpha$$, um den das Rechteck ABCD aus der horizontalen Lage gedreht ist
- die x-Koordinate $$a$$ des Eckpunkts $$A$$
$$b$$, $$c$$, $$d$$ seien die x-Koordinaten der übrigen Ecken $$B$$, $$C$$, $$D$$.
Wir betrachten den Fall,
dass $$\alpha$$ positiv ist und so klein, dass $$c$$ nicht links von $$a$$ liegt;
das ist gleichbedeutend mit $$u\leq v$$.
Zur Abkürzung setzen wir
$$u=a-d=b-c$$,
$$v=c-d=b-a$$,
$$s=AE=FC$$,
$$z=\dfrac{s}{2u}$$.
$$\mathcal{A_{\triangle}}$$ bezeichne die Fläche von $$\triangle AED$$ bzw. $$\triangle CFB$$.
Man liest ab:
$$u=p \sin \alpha \quad$$ und $$\quad v=q \cos \alpha$$.
(Die obige Voraussetzung $$u\leq v$$ ist somit gleichbedeutend mit
$$\tan \alpha \leq \dfrac{q}{p}$$, also $$\quad \alpha \leq \arctan \dfrac{q}{p}$$.)
Ferner ist
$$s=\dfrac{p}{\cos \alpha}$$, daher
$$\mathcal{A_{\triangle}} = \frac{1}{2} su = \frac{1}{2}p^2 \tan \alpha$$
und folglich
$$z = \dfrac{\mathcal{A_{\triangle}}}{u^2} = \dfrac{1}{2\cos\alpha \sin\alpha}$$.
$$x$$ sei die Stelle, bei der die vertikale Schnittgerade die x-Ache schneidet.
Die gesuchte Funktion $$f$$ für den grünen Flächenteil hat auf den durch $$0$$, $$a$$, $$b$$, $$c$$, $$d$$ und $$w$$ begrenzten Teilintervallen unterschiedliche Funktionsterme - abwechselnd lineare und quadratische.
(Wir nehmen jeweils die geschlossenen Teilintervalle als Definitionsmenge; an den gemeinsamen Trennstellen a, b, c, d stimmen jeweils die Funktionswerte der benachbarten Teilfunktionen überein: f ist überall stetig!)
Ich habe folgende Teilfunktionen gefunden:
Intervall $$[0; d]$$:
$$\quad f_{1}(x) = hx$$
Intervall $$[d; a]$$:
$$\quad f_{2}(x) = hx -z(x-d)^2$$
Intervall $$[a; c]$$:
$$\quad f_{3}(x) = (h-s)x + \frac{1}{2}s(d+a)$$
Intervall $$[c; b]$$:
$$\quad f_{4}(x) = z(b-x)^2 + hx - pq$$
Intervall $$[b; w]$$:
$$\quad f_{5}(x) = hx - pq$$
Die anderen Fälle
lassen sich durch Spielen mit der Geogebra-Zeichnung inspizieren, von der das obige Bild einen Zustand zeigt: https://www.geogebra.org/m/ad5bcanp
Mit den Schiebereglern lassen sich die Werte der gegebenen Größen variieren (insbesondere natürlich $$\alpha$$), der Punkt A lässt sich vertikal verschieben. (Freilich muss man darauf achten, dass das kleine Rechteck nicht aus dem großen herausragt.)
Der x-Wert der roten Schnittlinie lässt sich durch Verschieben des roten Punktes ändern.
Man erkennt, welche Änderungen gegenüber dem oben behandelten Fall nötig wären - im wesentlichen ist die Situation die gleiche.
Vielleicht hats ja doch noch jemand interessant gefunden...
Viele Grüße und ein schönes Wochenende
ottogal