Hallo in die Runde!
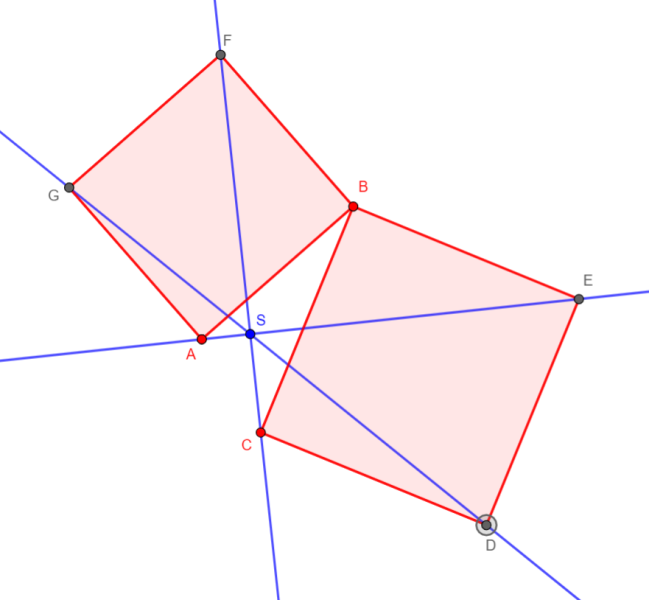
Gegeben sind zwei Quadrate $$ABFG$$ und $$BCDE$$, die die Ecke $$B$$ gemeinsam haben (ansonsten jedoch beliebig liegen können):
Man beweise: Die Verbindungsgeraden $$AE$$, $$CF$$ und $$DG$$ schneiden sich in einem Punkt $$S$$.
Naja, ein Bild sagt mehr als tausend Worte. Mir reicht ehrlich gesagt die schöne Abbildung als Beweis.