Mathematik zur Wochenmitte
- mathematik
Hallo in die Runde!
Gegeben sind zwei Quadrate $$ABFG$$ und $$BCDE$$, die die Ecke $$B$$ gemeinsam haben (ansonsten jedoch beliebig liegen können):
Man beweise: Die Verbindungsgeraden $$AE$$, $$CF$$ und $$DG$$ schneiden sich in einem Punkt $$S$$.
Viele Grüße
ottogal
Hallo in die Runde!
Gegeben sind zwei Quadrate $$ABFG$$ und $$BCDE$$, die die Ecke $$B$$ gemeinsam haben (ansonsten jedoch beliebig liegen können):
Man beweise: Die Verbindungsgeraden $$AE$$, $$CF$$ und $$DG$$ schneiden sich in einem Punkt $$S$$.
Naja, ein Bild sagt mehr als tausend Worte. Mir reicht ehrlich gesagt die schöne Abbildung als Beweis.
Hallo ottogal,
das ist ein verflixt gemeines Ding. Viele Winkel sehen gleich aus, aber bei genauerem Hinsehen (oder verschieben der Punkte) sind immer ein paar Grad Unterschied drin. Von ein paar Ausnahmen abgesehen, deren Existenz mir aber noch unerklärlich ist und von denen ich nichtmal weiß, ob sie für die Lösung relevant sind.
Ohne Geogebra wäre die "Lösungsforschung" echt die Hölle…
Rolf
Ich will seit zwei Tagen darüber nachdenken, hoffe am langen Wochenende schaffe ich es.
Wär also schön wenn die Lösung noch nicht so schnell kommt 😀
Klar doch! Viel Erfolg!
Teil-Lösung:
In der hier verlinkten Geogebra-Zeichnung
https://www.geogebra.org/m/ytuepgp6
lassen sich die roten Punkte A, B und C verschieben.
Dreht man das $$\triangle{AEB}$$ mit Drehpunkt $$B$$ um 90° im Uhrzeigersinn, so erhält man das $$\triangle{FCB}$$.
Dabei ist auch die Gerade $$AE$$ um 90° gedreht worden auf die Gerade $$FC$$; die beiden Geraden stehen also aufeinander senkrecht. Ihren Schnittpunkt nennen wir $$S$$. Es gilt also insbesondere $$\angle{FSA} = \angle{CSE} = 90°$$.
Zu zeigen bleibt: Die Punkte $$D$$, $$S$$ und $$G$$ liegen auf einer Geraden.
Man betrachte die Umkreise $$k_1$$ bzw. $$k_2$$ der Quadrate $$ABFG$$ und $$BCDE$$ mit ihren Mittelpunkten $$M_1$$ bzw. $$M_2$$.
Wir verwenden den Zusammenhang zwischen Umfangswinkel $$\phi = \angle{APB}$$ und Mittelpunktswinkel $$\mu = \angle{AMB}$$ einer Kreis-Sehne $$[AB]$$
(so genannter Kreiswinkelsatz):
Genau dann liegt $$P$$ auf der Kreislinie, wenn $$\mu = 2 \cdot \phi$$ ist:
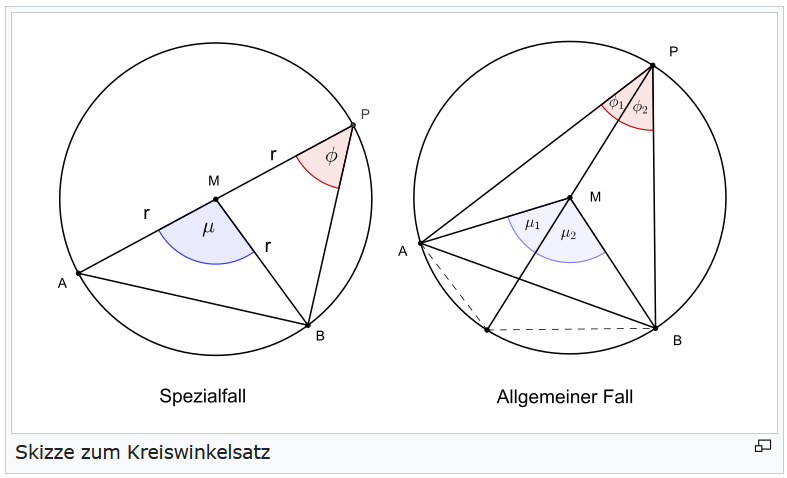
(Siehe Kreiswinkelsatz_(Zentriwinkelsatz) ).
Der Thales-Satz und seine Umkehrung sind ein Spezialfall hiervon: Falls $$[AB]$$ Durchmesser ist, wird $$\mu = 180°$$, und $$C$$ liegt genau dann auf der Kreislinie, wenn $$\phi = 90°$$ ist.
Damit ziehen wir folgende Schlüsse:
Weil $$[FA]$$ Durchmesser von $$k_1$$ und $$\angle{FSA} = 90°$$ ist, muss $$S$$ auf $$k_1$$ liegen.
Im Kreis $$k_1$$ gehört zur Sehne $$[FG]$$ der Mittelpunktswinkel $$\angle{FM_1G} = 90°$$,
also der Umfangswinkel $$\angle{FSG} = 45°$$.
Weil $$[CE]$$ Durchmesser von $$k_2$$ und $$\angle{CSE} = 90°$$ ist, muss $$S$$ auf $$k_2$$ liegen.
Im Kreis $$k_2$$ gehört zur Sehne $$[CD]$$ der Mittelpunktswinkel $$\angle{CM_2D} = 90°$$,
also der Umfangswinkel $$\angle{CSD} = 45°$$.
Es ist also $$\angle{FSG} = \angle{CSD}$$, und weil $$C$$, $$S$$ und $$F$$ auf einer Geraden liegen, muss das auch für $$D$$, $$S$$ und $$G$$ gelten.
Anmerkung:
Die Argumentation bleibt gültig, solange man in der abgebildeten Ausgangslage z.B. den Punkt $$C$$ nur so weit bewegt, dass $$S$$ auf dem Bogen $$AB$$ (ohne Endpunkte) bleibt.
Für andere Fälle muss man die Beweisführung modifizieren.
Dies sei dem interessierten Leser als (mühselige) Übung überlassen...
Hallo ottogal,
Dies sei dem interessierten Leser als (mühselige) Übung überlassen...
Ich bin eigentlich nicht interessiert…
Es reicht, A und B fest aber beliebig zu wählen - außer A=B - und mögliche Zonen für C zu betrachten. Einige dieser Zonen sind einzelne Punkte. Würde man C und B festhalten und A variieren, würde die Argumentation gespiegelt verlaufen.
Nö. Das guck ich mir lieber live mit Geogebra an und glaube, dass es stimmt 😉. Aber vielleicht findet ja jemand eine ganz andere, viel schlauere Überlegung, die diese Fallunterscheidungen obsolete macht.
Rolf
Dies sei dem interessierten Leser als (mühselige) Übung überlassen...
Ich bin eigentlich nicht interessiert…
...
Dafür hast du dir aber ganz schön viel Mühe gemacht!
...
Nö. Das guck ich mir lieber live mit Geogebra an und glaube, dass es stimmt 😉.
Geogebra macht leider gar keinen Spaß mehr, seit es bei mir unter Windows 11 nicht mehr vernünftig funktioniert...
Aber vielleicht findet ja jemand eine ganz andere, viel schlauere Überlegung, die diese Fallunterscheidungen obsolete macht.
Ja. Auf solch einen Einfall warte ich noch ...
Rolf
Schönes Wochenende! ottogal
Nachtrag:
Manchmal sieht man vor lauter Wald den einen Baum nicht...
Man kann sich die ganzen Betrachtungen über 45°-Winkel schenken:
Oben haben wir gezeigt, dass $$S$$ auf jedem der beiden Quadrat-Umkreise liegt.
Daher sind nach Thales auch $$\angle{BSG}$$ und $$\angle{DSB}$$ rechte Winkel, somit $$\angle{DSG}$$ ein gestreckter. Also liegen $$D$$, $$S$$ und $$G$$ auf einer Geraden.