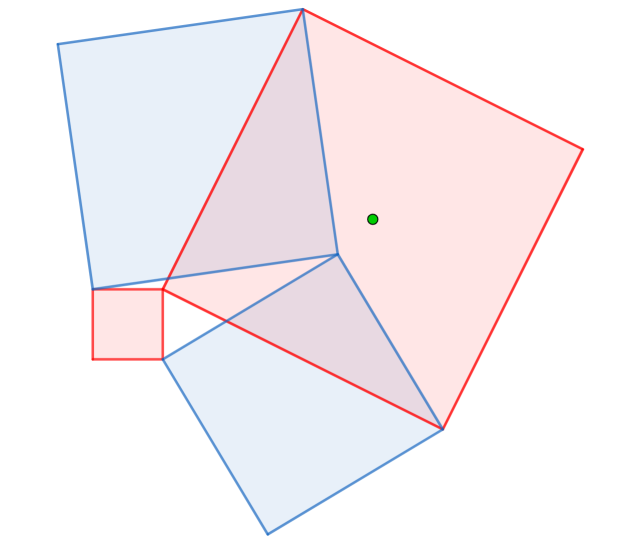
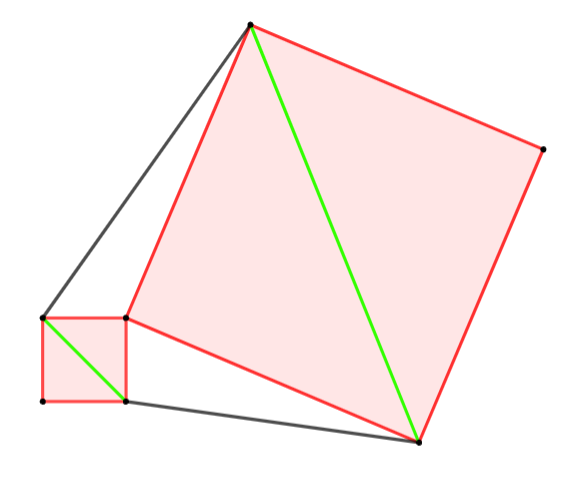
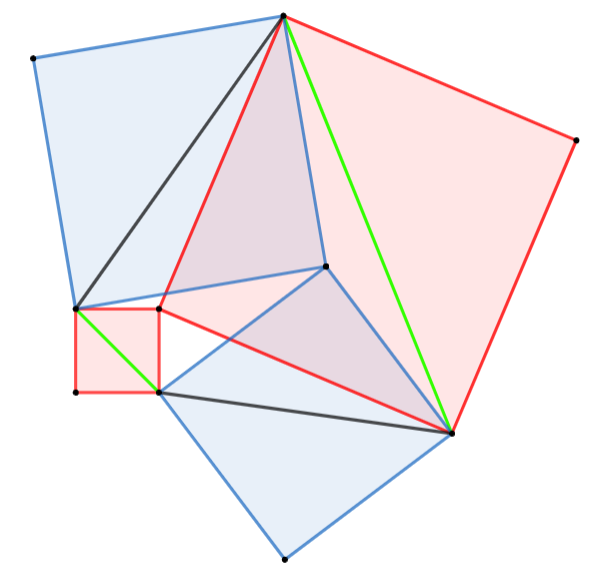
Dies ist ein Screenshot von folgendem Geogebra-Blatt:
https://www.geogebra.org/geometry/sfbvb4ym
Gegeben sind zwei (rote) Quadrate, die eine Ecke gemeinsam haben.
(Die Ausgangssituation ist also die selbe wie bei der Aufgabe vom 22.09.2022.
Die Ergebnisse von dort dürfen verwendet werden, werden aber nicht gebraucht.)
Das linke rote Quadrat liegt fest; das rechte roten Quadrat lässt sich durch Bewegen seines grünen Mittelpunkts variieren. Man beobachte die blauen Quadrate...
Dazu die folgende Aufgabe:
Grün markiert sind die beiden Quadratdiagonalen, die nicht durch die gemeinsame Ecke gehen. Ihre Endpunkte bilden ein Viereck.
Zu den anderen beiden Vierecksseiten gibt es je ein eindeutig bestimmtes Quadrat (blau), von dem sie eine Diagonale sind:
Man beweise folgende Behauptungen:
Behauptung 1:
Auch die beiden blauen Quadrate haben eine Ecke gemeinsam.
Behauptung 2:
Die Summe der Flächeninhalte der beiden roten Quadrate und die Summe der Flächeninhalte der beiden blauen Quadrate
stimmen überein.
Anmerkungen:
-
Fallunterscheidungen für die gegenseitige Lage der roten Quadrate sind nicht erforderlich; es genügt, den Beweis für die abgebildete Lage zu führen.
-
Es ist nicht ganz einfach; daher werde ich mit einer Lösung etwas länger hinterm Berg halten.