O.B.d.A. legen wir das erste rote Quadrat $$ABCD$$ fest in ein kartesisches Koordinatensystem derart, dass
$$\quad A(0|0)$$, $$B(-1|0)$$, $$C(-1|-1)$$ und $$D(0|-1) \quad$$ ist.
Sein Mittelpunkt ist dann $$\quad M_{1}(-\frac{1}{2}|-\frac{1}{2})$$.
Der Ursprung $$O = A(0|0)$$ sei die gemeinsame Ecke mit dem zweiten roten Quadrat $$OEFG$$.
Dessen Lage wird eindeutig bestimmt durch seinen (beliebig wählbaren) Mittelpunkt $$M_{2}$$ (grün).
Wir setzen $$\quad M_{2}(a|b) \quad$$ mit den Variablenn $$a$$ und $$b$$.
Die Diagonale durch $$A$$ hat somit den Endpunkt $$F(2a|2b)$$.
Wir beweisen nun allgemein einen Hilfssatz, den wir dann mehrfach anwenden.
Behauptung:
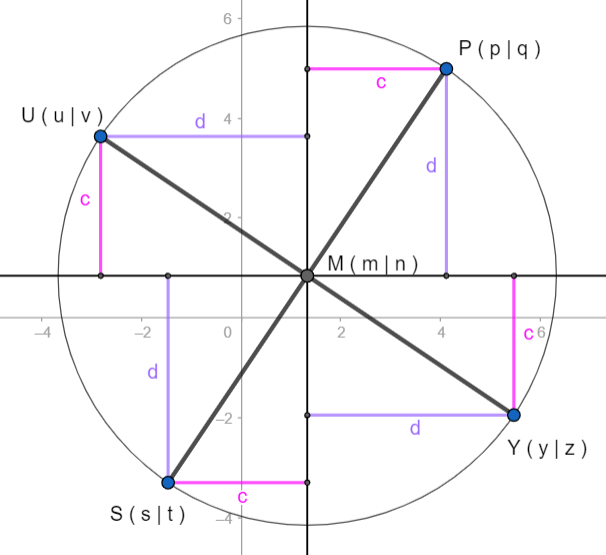
Seien $$P(p|q)$$ und $$S(s|t)$$ die Endpunkte einer Diagonalen eines Quadrats,
so gilt für die anderen beiden Eckpunkte $$U(u|v)$$ und $$Y(y|z)$$:
$$u = \frac{1}{2}( p-q+s+t )$$
$$v = \frac{1}{2}( p+q-s+t )$$
$$y = \frac{1}{2}( p+q+s-t )$$
$$z = \frac{1}{2}(-p+q+s+t )$$.
Beweis:
Der Zeichnung entnimmt man
$$\quad u = m-d \quad$$ und $$\quad v= n+c \quad$$ sowie
$$\quad c=(p-s)/2 \quad$$ und $$\quad d=(q-t)/2 \quad$$.
Da die Koordinaten des Mittelpunkts $$M(m|n)$$ des Quadrats
$$m=(p+s)/2 \quad$$ und $$\quad n=(q+t)/2 \quad$$ sind,
erhält man durch Einsetzen die behaupteten Terme.
Wir wenden den Hilfssatz auf die Diagonale $$[OF]$$ an und erhalten
$$u = \frac{1}{2}( 0-0+2a+2b ) = a+b$$
$$v = \frac{1}{2}( 0+0-2a+2b ) = b-a$$
$$y = \frac{1}{2}( 0+0+2a-2b ) = a-b$$
$$z = \frac{1}{2}(-0+0+2a+2b ) = a+b$$.
Die andern beiden Ecken des gesuchten Quadrats sind also
$$E(a+b|b-a) \quad$$ und $$\quad G(a-b|a+b)$$.
Wir wenden nun den Hilfssatz auf die Strecke $$[DE]$$ an:
Mit $$D(0|-1)$$ statt $$P$$ und $$\quad E(a+b|b-a) \quad$$ statt $$S$$ erhalten wir
$$u = \frac{1}{2}( 0+1+a+b+b-a ) = b+\frac{1}{2}$$
$$v = \frac{1}{2}( 0-1-a-b+b-a ) = -a-\frac{1}{2}$$
$$y = \frac{1}{2}( 0-1+a+b-b+a ) = a-\frac{1}{2}$$
$$z = \frac{1}{2}(-0-1+a+b+b-a ) = b-\frac{1}{2}$$.
Die gesuchten Ecken des dritten Quadrats $$DK_{3}EH_{3}$$ (blau) sind also
$$\quad K_{3}(b+\frac{1}{2}|-a-\frac{1}{2}) \quad$$ und $$\quad H_{3}(a-\frac{1}{2}|b-\frac{1}{2})$$.
Entsprechend finden wir zu der Strecke $$[GB]$$ die übrigen Ecken des gesuchten vierten Quadrats $$BH_{4}GK_{4}$$ (blau):
Mit $$G(a-b|a+b)$$ statt $$P$$ und $$\quad B(-1|0) \quad$$ statt $$S$$ erhalten wir
$$u = \frac{1}{2}( a-b-a-b-1+0 ) = -b-\frac{1}{2}$$
$$v = \frac{1}{2}( a-b+a+b+1+0 ) = a+\frac{1}{2}$$
$$y = \frac{1}{2}( a-b+a+b-1-0 ) = a-\frac{1}{2}$$
$$z = \frac{1}{2}(-a+b+a+b-1+0 ) = b-\frac{1}{2}$$.
Die gesuchten Ecken sind also $$\quad K_{4}(-b-\frac{1}{2}|a+\frac{1}{2})$$ und $$\quad H_{4}(a-\frac{1}{2}|b-\frac{1}{2}) \quad$$.
Man sieht: Die Ecke $$H_{3}$$ des dritten Quadrats und die Ecke $$H_{4}$$ des vierten Quadrats fallen zusammen.
Damit ist Aussage 1 bewiesen.
Zu den Flächeninhalten:
Das erste rote Quadrat hat die Fläche $$Q_{1}=1$$.
Mit $$F(2a|2b)$$ und $$O(0|0)$$ folgt $$|OF|^2=4(a^2+b^2)$$.
Die Fläche des zweiten roten Quadrats $$OEFG$$ ist halb so groß, also $$Q_{2}=2(a^2+b^2)$$.
Wegen $$D(0|-1)$$ und $$H_{3}(a-\frac{1}{2}|b-\frac{1}{2})$$ folgt $$|DH_{3}|^2=(a-\frac{1}{2})^2+(b+\frac{1}{2})^2=a^2+b^2-a+b+\frac{1}{2}$$.
Das ist also die Fläche $$Q_{3}$$ des dritten Quadrats $$DK_{3}EH_{3}$$.
Wegen $$B(-1|0)$$ und $$H_{4}(a-\frac{1}{2}|b-\frac{1}{2}) \quad$$ folgt $$ \quad|BH_{4}|^2=(a+\frac{1}{2})^2+(b-\frac{1}{2})^2=a^2+b^2+a-b+\frac{1}{2}$$.
Das ist also die Fläche $$Q_{4}$$ des vierten Quadrats $$BH_{4}GK_{4}$$.
Es folgt $$Q_{3}+Q_{4}=2(a^2+b^2)+1=Q_{2}+Q_{1}$$.
Damit ist Aussage 2 bewiesen.
Viele Grüße
ottogal