Mathematik zum Wochenende - Weiteres zur Lösung.

[ottogal]

Egal, wie man vorgeht, man muss einen Weg finden, einen Vektor um 90° zu drehen.

Wenn man in seiner Werkzeugkiste auch die Komplexen Zahlen hat, erinnert man sich:
In $$\mathbb {C} $$ ist die Drehung des zu einer komplexen Zahl $$z$$ gehörenden Ortsvektors um +90° einfach eine Multiplikation von $$z$$ mit der imaginären Einheit $$\mathrm{i}$$ (bzw. mit $$-\mathrm{i}$$ bei Drehung um -90°).

---

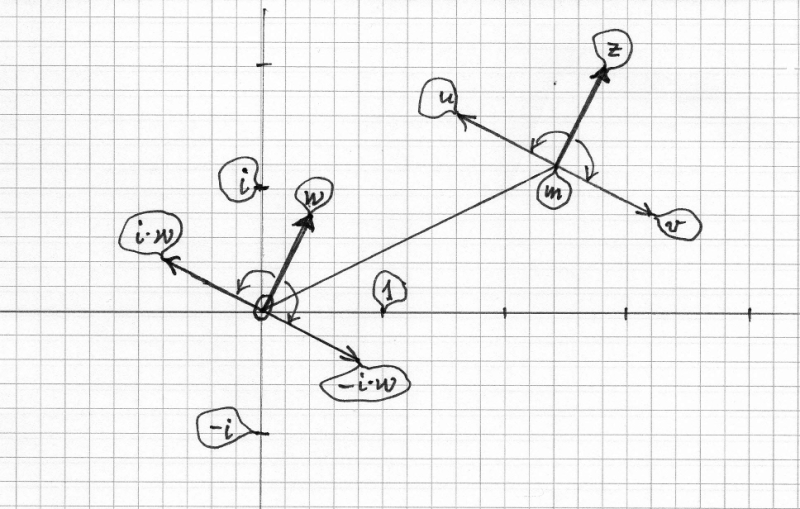
Gegeben seien zwei verschiedene komplexe Zahlen $$m=c+\mathrm{i}d$$ und $$z=x+\mathrm{i}y$$. Mit einer Translation bringt man $$m$$ in den Ursprung und $$z$$ nach $$w = z-m$$.

Drehung von $$w$$ um den Ursprung um +90° ergibt (wegen $$\mathrm{i}^2=-1$$)

$$\mathrm{i}w= \mathrm{i}(z-m) = \mathrm{i}(x-c)+i^2(y-d) = \mathrm{i}(x-c)-(y-d)$$, also
$$\mathrm{i}w= (d-y) +\mathrm{i}(x-c)$$.

Dreht man dagegen um -90°, erhält man den Gegenvektor dazu:

$$-\mathrm{i}w=(y-d)+\mathrm{i}(c-x)$$.

Nun verschieben wir alles wieder vom Ursprung nach $$m$$ und erhalten

$$u = \mathrm{i}w + m =(d-y+c)+\mathrm{i}(x-c+d)$$ und
$$v = -\mathrm{i}w+m = (y-d+c)+\mathrm{i}(c-x+d)$$.

---

Das wenden wir nun auf unsere Aufgabe an; ich bezeichne die Punkte wie in meiner Skizze.

Quadrat $$Q_{2}$$:

Hier nehmen wir den Vektor $$\overrightarrow{M_{2}F}$$,
haben also $$c=a$$, $$d=b$$, $$x=2a$$, $$y=2b$$.
Wir erhalten
$$u=(b-2b+a)+\mathrm{i}(2a-a+b) = (a-b)+\mathrm{i}(a+b)$$ und
$$v=(2b-b+a)+\mathrm{i}(a-2a+b) = (a+b)+\mathrm{i}(b-a)$$.

Das sind also die Ecken $$G$$ und $$E$$.

Quadrat $$Q_{3}$$:

Hier nehmen wir den Vektor $$\overrightarrow{M_{3}D}$$,
haben also $$c=\frac{1}{2}(a+b)$$, $$d=\frac{1}{2}(b-a-1)$$, $$x=0$$, $$y=-1$$.
Wir erhalten (gleich vereinfacht)
$$u= (b+\frac{1}{2})+\mathrm{i}(-a-\frac{1}{2})$$ und
$$v= (a-\frac{1}{2})+\mathrm{i}(b-\frac{1}{2})$$.

Das sind also die Ecken $$K_{3}$$ und $$H_{3}$$.

Quadrat $$Q_{4}$$:

Hier nehmen wir den Vektor $$\overrightarrow{M_{4}B}$$,
haben also $$c=\frac{1}{2}(a-b-1)$$, $$d=\frac{1}{2}(a+b)$$, $$x=-1$$, $$y=0$$.
Wir erhalten diesmal $$u= (a-\frac{1}{2})+\mathrm{i}(b-\frac{1}{2})$$ und
$$v= (-b-\frac{1}{2})+\mathrm{i}(a+\frac{1}{2})$$.

Das sind also die Ecken $$H_{4}$$ und $$K_{4}$$.

Vergleich ergibt die Übereinstimmung von $$H_{3}$$ und $$H_{4}$$.

q.e.d.