Hallo Gunnar,

da Du deine Tangens-Lösung getwittert hast, und mein Bild eh schon der Katze eine Dreiecksrasur verpasst hat, kann ich sie auch aus dem Sack lassen.

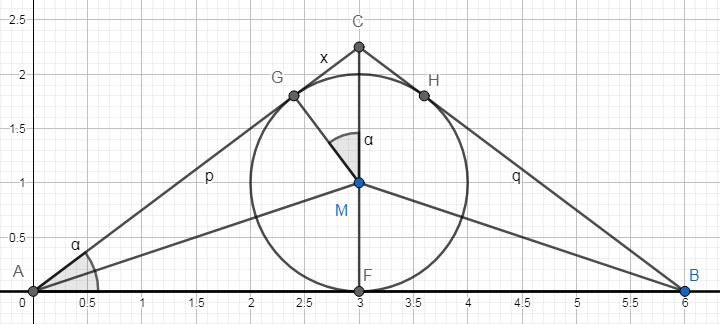
G und H sind die Berührpunkte des Inkreises mit den Seiten AC und CB. Sei h noch die Höhe FC des Dreiecks ABC (im Bild nicht bezeichnet).

Die Strecken AG und BH haben die Länge 3, weil AC/AB sowie BF/BC Tangenten aus dem gleichen Punkt sind. Die rechtwinkligen Drachen AFMG und BFMH (MH ist nicht gezeichnet) haben demnach jeweils die Fläche 3r = 3. Es bleibt die Frage nach dem verbleibenden kleinen Drachen MHCG. Bei diesem hat ein Seitenpaar die Länge r=1, die andere Seite x ist zu bestimmen.

Weil MG auf AC senkrecht steht und CF auf AB, sind die bei M und A gezeichneten Winkel gleich. Die rechtwinkligen Dreicke AFC und CGM sind damit ähnlich. Damit verhält sich

$$\displaystyle \frac{h}{3} = \frac{x}{1}$$

woraus folgt:

$$h=3x$$ (1)

Matthias Apsel schlug mir Pythagoras vor: $x²+1² = (h-1)²$, ich wollte aber auf Quadrate verzichten und wendete darum ein weiteres Verhältnis aus der Ähnlichkeit der Dreiecke an:

$$\displaystyle \frac{MC}{MG} = \frac{AC}{AF}$$

mit eingesetzten Werten

$$\displaystyle \frac{h-1}{1}=\frac{3+x}{3}$$ (2)

Einsetzen von (1) führt zu

$$\begin{aligned} & & 3x-1 &= 1+\frac{x}{3}
\Longleftrightarrow & & \frac{8}{3}x &= 2
\Longleftrightarrow & & x &= \frac{3}{4} \end{aligned}$$

Daraus berechnet sich die Fläche des kleinen Drachen zu 0,75.

Was aber eigentlich viel zu umständlich war. Wenn ich nämlich die Umkehrung von (1), also $$x=\frac{h}{3}$$, in (2) einsetze, bekomme ich $$\frac{h-1}{1}=\frac{3+\frac{h}{3}}{3} \Longleftrightarrow h-1=1+\frac{h}{9} \Longleftrightarrow \frac{8}{9}h=2 \Longleftrightarrow h=\frac{9}{4}$$, und daraus kann ich mit $$A=\frac{1}{2}\cdot 6 \cdot h = 3\cdot \frac{9}{4} = \frac{27}{4} = 6{,}75$$ die Fläche direkt berechnen, ohne große und kleine Drachen töten zu müssen.

Look Ma, no tangent!

Rolf