Mathematik zum Wochenende
- mathematik
0  Gunnar Bittersmann
Gunnar Bittersmann
0  Matthias Apsel
Matthias Apsel
0  Rolf b
Rolf b
0 Mathematik zum Wochenende - Vorsicht Spoiler!
 encoder
encoder
Hallo alle,
heute wieder Geometrie, allerdings einfach. Nichts für Gunnar[1]. Er wollte ja stattdessen Mathematik zum Monatsende liefern.
In ein bei C rechtwinkliges Dreieck ABC wird ein Quadrat einbeschrieben. (siehe Skizze)
Bestimme eine Gleichung für die Seitenlänge q des Quadrats in Abhängigkeit der Kathetenlängen a und b.
Bis demnächst
Matthias
Er darf natürlich trotzdem mitmachen ;-) ↩︎
@@Matthias Apsel
Er darf natürlich trotzdem mitmachen ;-)
Hab ich dann mal. Aufgabe zum WE heißt aber nicht, dass das WE schon vorbei ist, wenn man die Aufgabe gelöst hat, oder?
Sonst hätte das WE nicht 2 Tage, sondern nur 2 Minuten – wenn man’s geschickt anstellt.
LLAP 🖖
@@Gunnar Bittersmann
Sonst hätte das WE nicht 2 Tage, sondern nur 2 Minuten – wenn man’s geschickt anstellt.
Solll heißen: Wenn man sich die Aufgabe zurechtbiegt, ist die Lösung ein Klacks.
Die Herausvorderung besteht im Zurechtbiegen.
LLAP 🖖
Hallo Gunnar Bittersmann,
Solll heißen: Wenn man sich die Aufgabe zurechtbiegt, ist die Lösung ein Klacks.
Die Herausvorderung besteht im Zurechtbiegen.
Für die Altforderen? ;-)
Ich bin auf die Biegung gespannt und mach jetzt die Biege innss Bettt ;-)
Bis demnächst
Matthias
Ich habe sie nicht verbogen, sondern verdreht und umgeklappt und dann war's auch ein Klax.
:) Rolf
@@Rolf b
Ich habe sie nicht verbogen, sondern verdreht und umgeklappt und dann war's auch ein Klax.
Ich wollte ja nicht gleich mit der Drehtür ins Haus fallen. ;-)
LLAP 🖖
Hallo Gunnar Bittersmann,
Sonst hätte das WE nicht 2 Tage, sondern nur 2 Minuten – Wenn man’s geschickt anstellt.
Ich hab über geschickte Varianten nicht nachgedacht. Auch straight forwards dauert es nicht länger als 2 Minuten.
Bis demnächst
Matthias
@@Matthias Apsel
Ich hab über geschickte Varianten nicht nachgedacht. Auch straight forwards dauert es nicht länger als 2 Minuten.
Ich bin dann bei der Auflösung gespannt, wie deine Straight-forwards-Lösung aussieht.
LLAP 🖖
Hallo Matthias Apsel,
In ein bei C rechtwinkliges Dreieck ABC wird ein Quadrat einbeschrieben. (siehe Skizze)
Bestimme eine Gleichung für die Seitenlänge q des Quadrats in Abhängigkeit der Kathetenlängen a und b.
Wenn man q bestimmt hat, ist es relativ leicht zu zeigen, dass das Quadrat höchstens halb so groß wie das Dreieck ist.
Wie?
Geht das auch ohne Kenntnis von q?
Bis demnächst
Matthias
@@Matthias Apsel
Geht das auch ohne Kenntnis von q?
Ja. Nette Aufgabe.
LLAP 🖖
Hallo Gunnar Bittersmann,
Nette Aufgabe.
😄
Bis demnächst
Matthias
Hallo Gunnar Bittersmann,
Ja.
Stimmt. Und schick.
Bis demnächst
Matthias
Hallo Matthias Apsel,
Geht das auch ohne Kenntnis von q?
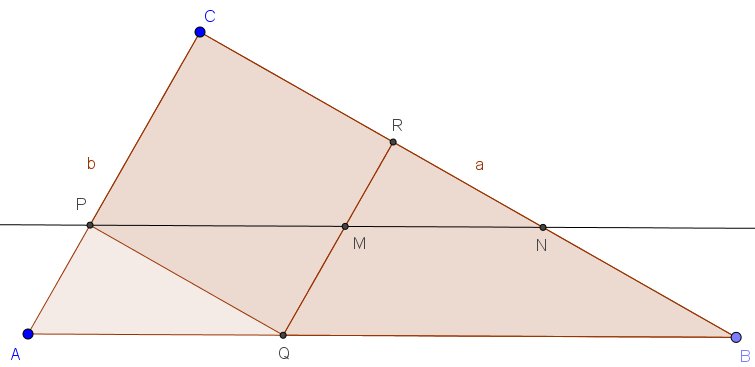
Das Dreieck ABC wird gebildet durch das Quadrat PQRC und die beiden ähnlichen Dreiecke QBR und AQP. Ohne Beschränkung der Allgemeinheit sei a > b.
Als Hilflinie verwenden wir eine Parallele zur Hypotenuse c durch den Punkt P.
Die Dreiecke AQP und MPQ sind kongruent, ebenso die Dreiecke QBR und PNC.
Das Dreieck PNC ist größer als das Trapez PMRC (wegen a > b ist auch CN > CR, mithin liegt R zwischen C und N, wegen der Parallelität von PC und MR liegt M zwischen P und N)
Damit sind die Dreiecke QBR und AQP stets größer als das Quadrat.
Für das gleichschenklig-rechtwinklige Dreieck ABC wären P und N die Mittelpunkte der Katheten und Q der Mittelpunkt der Hypotenuse. Verbindet man die Mittelpunkte der Seiten eines Dreicks, so entstehen vier kongruente Dreiecke, zwei davon bilden das Quadrat. In diesem Fall ist das Quadrat also halb so groß wie das Dreieck ABC.
Bis demnächst
Matthias
wegen a > b ist auch CN > CR
Über dieses Detail musste ich etwas grübeln, weil es mir nicht offensichtlich erschien. Das Licht ging mir dann auf, weil $$ \overline{CR} = \overline{CP} $$ ist (Quadratkanten), und dann ergibt sich die Behauptung aus dem Strahlensatz: $$ \frac{\overline{CN}}{\overline{CP}} = \frac{a}{b} > 1 \Longrightarrow \overline{CN} > \overline{CP}$$.
Rolf
Hallo Matthias Apsel,
Alternativ lässt sich noch eine weitere Hilfslinie hinzufügen, dann wird die Argumentation kürzer:
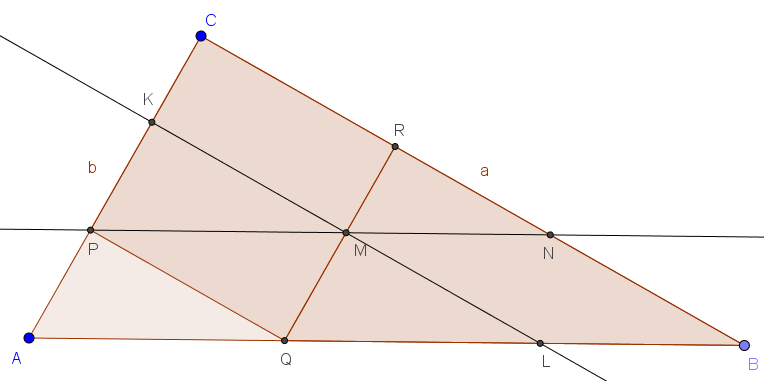
Das Quadrat wird in zwei Rechtecke zerlegt. PQMK hat den selben Flächeninhalt wie die Dreiecke AQP und QLM. Bleibt der Vergleich der Flächeninhalts des Rechtecks KMRC mit dem des Trapezes MLBR:
Beide haben dieselbe Höhe (MR), die Grundseite des Quadrates ist q, die kleinere der parallelen Seiten des Trapezes ist auch q. Deshalb hat das Trapez den größeren Flächeninhalt.
Bis demnächst
Matthias
Auch nicht schlecht. Wie bettet man eigentlich eigene Bilder ein (ohne sie fremdzuhosten)? Oder braucht es dazu eine eigene Berechtigung?
Hallo Rolf b,
Auch nicht schlecht. Wie bettet man eigentlich eigene Bilder ein (ohne sie fremdzuhosten)? Oder braucht es dazu eine eigene Berechtigung?
JavaScript zulassen ;-)
Dann steht unter der Antwort-textarea „Bilder hierher ziehen oder klicken, um sie hochzuladen. Beachten Sie die Nutzungsbedingungen.“
Bis demnächst
Matthias
@@Matthias Apsel
Alternativ lässt sich noch eine weitere Hilfslinie hinzufügen, dann wird die Argumentation kürzer:
Ich glaube, ich komme mit weniger Hilflinien und noch kürzerer Argumentation aus:
O.B.d.A. sei AC ≥ BC. Bezeichnung der Punkte siehe Skizze:[1]
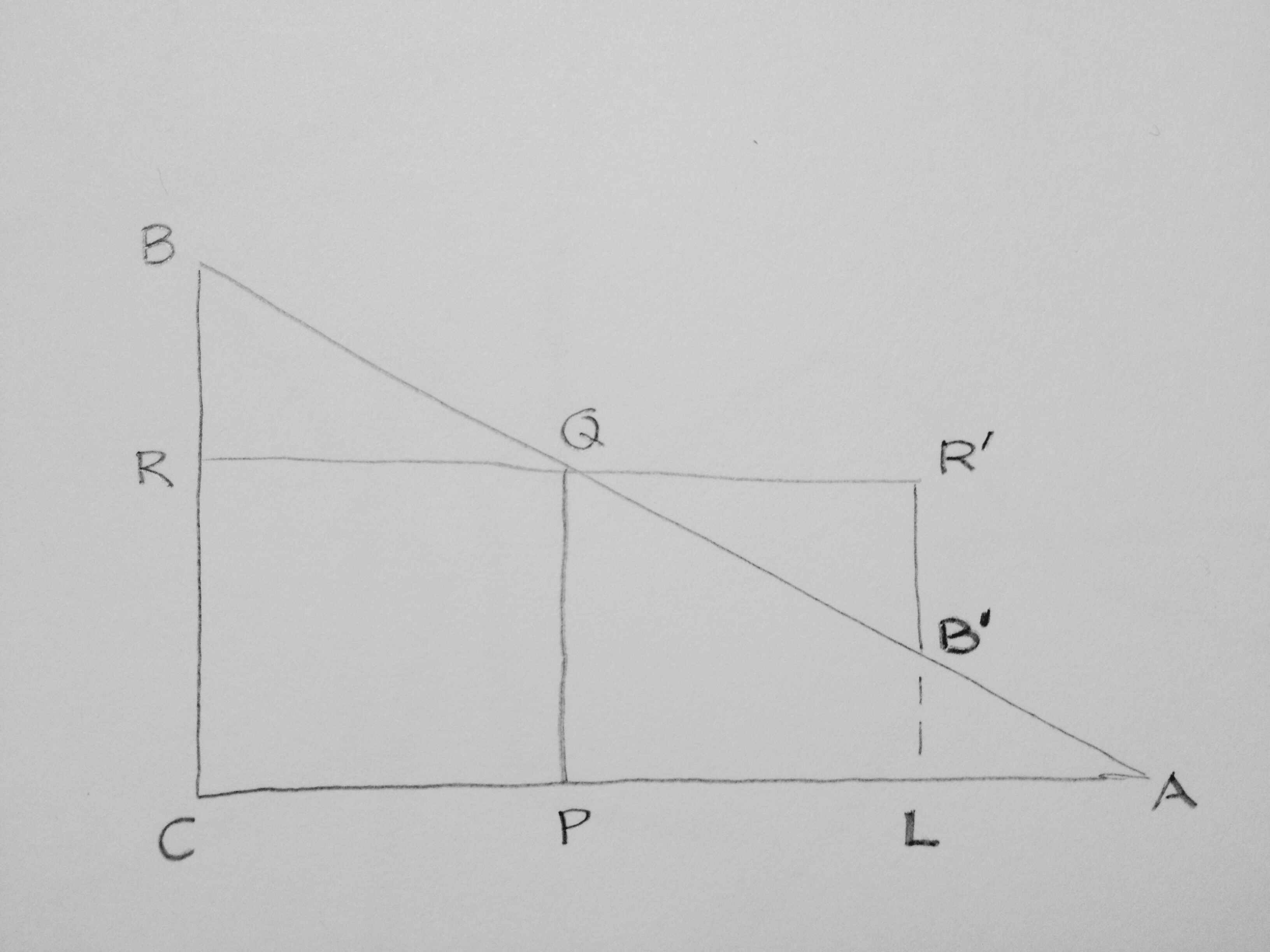
Das Dreieck QBR wird an Q gespiegelt (d.h. um 180° um Q gedreht). Für AC > BC liegt L zwischen P und A; für AC = BC fällt L mit A zusammen. Die Quadrate CPQR und PLRʹQ sind flächengleich.
Die Restfläche des Dreiecks ABC ohne das Quadrat CPQR ist flächengleich dem Quadrat PLRʹQ plus (für AC > BC) dem Dreieck LABʹ; somit mindestens so groß wie das Quadrat CPQR, d.h. das Quadrat CPQR ist höchstens halb so groß wie das Dreieck ABC.
LLAP 🖖
Nicht barrierefrei, ich weiß. Grmpf. ↩︎
Hallo Gunnar Bittersmann,
Geschickt!
Bis demnächst
Matthias
Genau diese Argumentation (mit der Punktspiegelung von RQB) wollte ich auch verfolgen. Matthias hat eine Nachricht vor mir, wo's drinsteht, nur ohne Skizze und deshalb mit vielen Worten formuliert.
Aber ich fand es nicht offensichtlich, weshalb L innerhalb von PA liegt. Optisch ist es klar, aber Mathe geht anders. In meiner Zeichnung habe ich den Grund nicht gesehen, in deiner schon :)
Es ist q = PL = PQ. Laut Strahlensatz ist QP/PA = b/a, und weil b<a ist QP<PA.
Rolf
@@Matthias Apsel
In ein bei C rechtwinkliges Dreieck ABC wird ein Quadrat einbeschrieben. (siehe Skizze)
Bestimme eine Gleichung für die Seitenlänge q des Quadrats in Abhängigkeit der Kathetenlängen a und b.
Über den Strahlensatz kommt man wie gesagt auch dahin, aber ein rechtwinkliges Dreieck ist prädestiniert dafür, so in ein rechtwinkliges Koordinatensystem gelegt zu werden, dass der Scheitel des rechten Winkels im Ursprung und die Katheten auf den positiven Teilen der Achsen liegen:
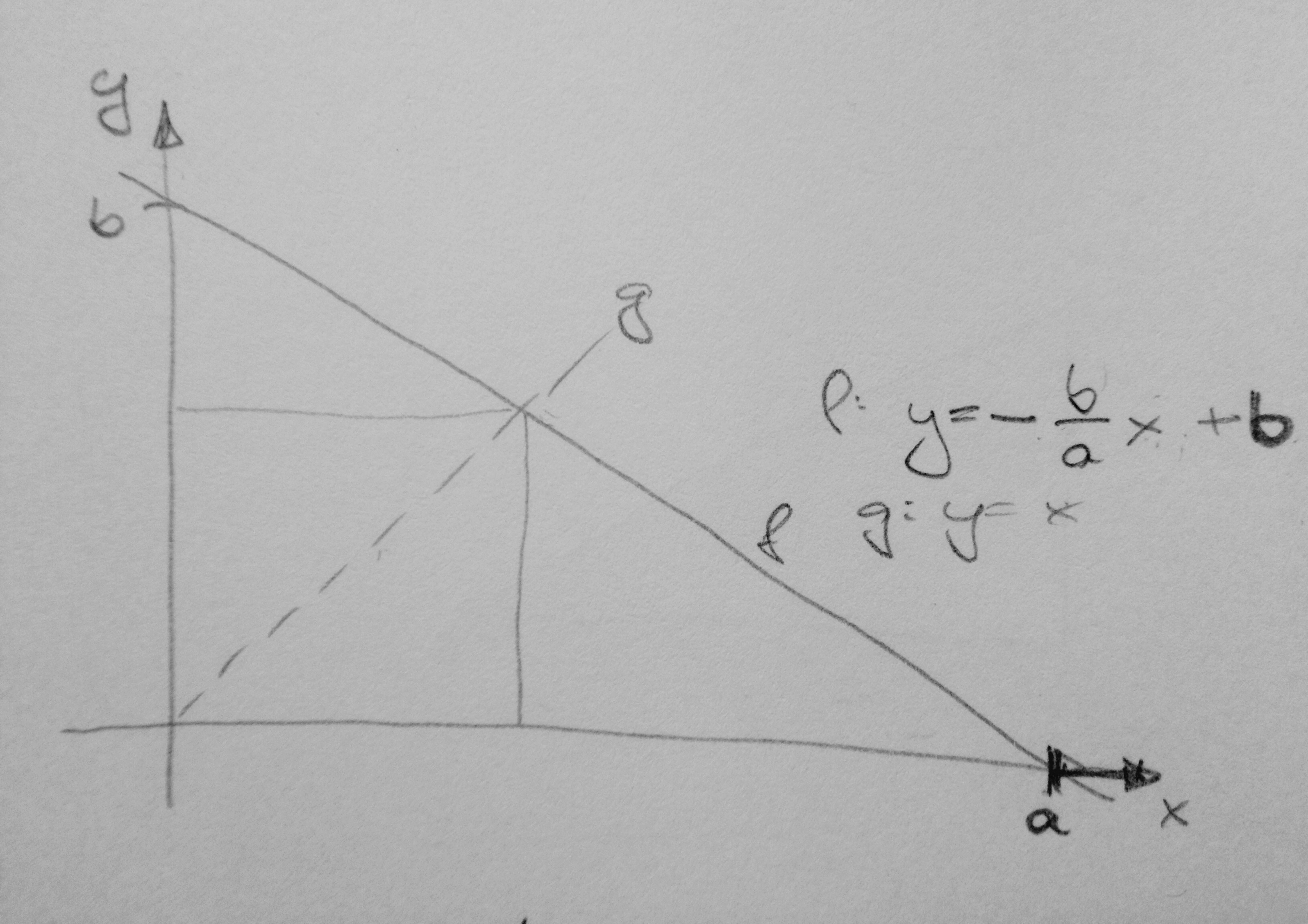
Die Geradengleichung der Hypotenuse ist dann $$y = -\frac{b}{a} x + b$$
Das Quadrat hat dann ebenfalls zwei Seiten auf den Achsen des Koordinatensystems und einen Eckpunkt in dessen Urprung. Der diesem gegenüberliegende Eckpungt liegt auf der Geraden $$y = x$$, folglich $$x = -\frac{b}{a} x + b$$, was für $$x = \frac{ab}{a + b} = q$$ erfüllt wird.
Wenn man q bestimmt hat, ist es relativ leicht zu zeigen, dass das Quadrat höchstens halb so groß wie das Dreieck ist.
Wie?
Für alle positiven a, b gilt $$\qquad\qquad\quad 0 \le ab \left( a - b \right) ^2 = ab \left( a^2 - 2ab + b^2 \right)$$
Durch Addition von 4_a_²_b_² erhält man $$\quad 4a^2b^2 \le ab \left( a^2 + 2ab + b^2 \right) = ab \left( a + b \right) ^2$$
Die Division durch 4(a + b)² > 0 ergibt $$\quad q^2 = \frac{a^2b^2}{\left( a + b \right) ^2} \le \frac{1}{4} ab$$
Auf der linken Seite steht nun gerade die Fläche des Quadrats; auf der rechten die Hälfte der Fläche des Dreiecks.
Geht das auch ohne Kenntnis von q?
Ja. Und das ist dann auch einfacher: geometrisch.
LLAP 🖖
Hallo Gunnar Bittersmann,
Geht das auch ohne Kenntnis von q?
Ja. Und das ist dann auch einfacher: geometrisch.
Und auch nicht geometrisch.
Der auf der Hypotenuse liegende Eckpunkt des Quadrates teilt diese in zwei Abschnitte u und v, der an A liegende Hypotenusenabschnitt sei u.
Wir zeigen, dass die Fläche $$A_R$$ der beiden kleinen Dreiecke größer oder gleich der Quadratfläche ist.
Es gilt
$$\begin {align}
A_R & = \frac{1}{2}qu \sin \beta + \frac{1}{2}qv \sin \alpha\
& = \frac{1}{2}qu \frac{q}{v} + \frac{1}{2}qv \frac{q}{u}\
& = \frac{1}{2}q^2 \left( \frac{u}{v} + \frac{v}{u} \right)
\end {align}$$
Der Term in der Klammer ist stets größer oder gleich 2. Wir erinnern uns?
q.e.d.
Bis demnächst
Matthias
Hallo Matthias Apsel,
In ein bei C rechtwinkliges Dreieck ABC wird ein Quadrat einbeschrieben. (siehe Skizze)
Ein Eckpunkt des Quadrates teilt die Hypotenuse in die Abschnitte[1] u und v.
Man zeige, dass gilt:
$$q^2 = \frac{\left( uv\right) ^2}{u^2+v^2}$$
Bis demnächst
Matthias
Ich weiß gar nicht, ob der Begriff Hypotenusenabschnitt für die beiden reserviert ist, die durch die Höhe entstehen. Wäre denkbar, sollte aber nicht, imho. ↩︎
@@Matthias Apsel
Ich weiß gar nicht, ob der Begriff Hypotenusenabschnitt für die beiden reserviert ist, die durch die Höhe entstehen.
Aber die heißen doch p und q, nicht u und v!!1elf *duckundweg*
Jetzt sitz ich schon 5 Minuten an der Aufgabe und hab’s immer noch nicht. Ich brauch erstmal eine Pause von der Frühstückspause.
LLAP 🖖
@@Gunnar Bittersmann
Ein Eckpunkt des Quadrates teilt die Hypotenuse in die Abschnitte[^1] u und v.
Man zeige, dass gilt:
$$q^2 = \frac{\left( uv\right) ^2}{u^2+v^2}$$
Jetzt sitz ich schon 5 Minuten an der Aufgabe und hab’s immer noch nicht. Ich brauch erstmal eine Pause von der Frühstückspause.
Jetzt aber Schluss mit Pause!
Wir erinnern uns:
$$q = \frac{ab}{a + b}$$
Pythagoras rausgekramt:
$$\begin{align} u^2 & = \left( a - q \right)^2 +q^2
& = a^2 - 2aq + 2q^2
& = a^2 - 2a \frac{ab}{a+b} + 2 \frac{a^2 b^2}{\left( a + b \right)^2}
& = \frac{a^2 \left( a + b \right)^2}{\left( a + b \right)^2} - \frac{2a^2b \left( a + b \right)}{\left( a + b \right)^2} + \frac{2a^2b^2}{\left( a + b \right)^2}
& = \frac{a^4 + 2a^3b + a^2b^2 - 2a^3b - 2a^2b^2 + 2a^2b^2}{\left( a + b \right)^2}
& = \frac{a^4 + a^2b^2}{\left( a + b \right)^2}
& = \frac{a^2 \left(a^2 + b^2 \right)}{\left( a + b \right)^2} \end{align}$$
Analog:
$$v^2 = \frac{b^2 \left( a^2 + b^2 \right)}{\left( a + b \right)^2}$$
Mit
$$\begin{align}u^2 + v^2 & = \frac{\left( a^2 + b^2 \right) \left( a^2 + b^2 \right)}{\left( a + b \right)^2}
& = \frac{\left( a^2 + b^2 \right)^2}{\left( a + b \right)^2} \end{align}$$
ergibt sich
$$\begin{align}\frac{u^2v^2}{u^2 + v^2} & = \frac{a^2b^2 \left( a^2 + b^2 \right)^2}{\left( a + b \right)^4} \cdot \frac{\left( a + b \right)^2}{\left( a^2 + b^2 \right)^2}
& = \frac{a^2b^2}{\left( a + b \right)^2}
& = q^2 \end{align}$$
Jetzt sagt nicht, dass das auch einfacher ohne ellenlange Rechung geht!
LLAP 🖖
Hallo Gunnar Bittersmann,
Jetzt sagt nicht, dass das auch einfacher ohne ellenlange Rechung geht!
Doch, geht es. Als Tipp sei dir meine straight-forwards-Lösung ans Herz gelegt.
Bis demnächst
Matthias
@@Matthias Apsel
Jetzt sagt nicht, dass das auch einfacher ohne ellenlange Rechung geht!
Doch, geht es. Als Tipp sei dir meine straight-forwards-Lösung ans Herz gelegt.
Ach, man darf Winkelfunktionen verwenden‽‽ Ach ja, ist ja Mathematik zur Frühstückspause, nicht Mathematik zum Monatsende.
Meh, ein Einzeiler.
LLAP 🖖
Hallo Gunnar Bittersmann,
Meh, ein Einzeiler.
Nun ja, ich würde es in mehrere Zeilen schreiben.
Bis demnächst
Matthias
@@Matthias Apsel
Meh, ein Einzeiler.
Nun ja, ich würde es in mehrere Zeilen schreiben.
Naja, bei 3 Gleichheitszeichen passt’s noch in eine.
Obwohl: TIL wie man die Gleichheitszeichen mit LaTeX so schön untereinander bekommt. War die Frühstückspause doch zu was gut.
LLAP 🖖
Hallo Gunnar Bittersmann,
Naja, bei 3 Gleichheitszeichen passt’s noch in eine.
Ich bin auf deine Lösung gespannt.
Obwohl: TIL wie man die Gleichheitszeichen mit LaTeX so schön untereinander bekommt. War die Frühstückspause doch zu was gut.
Ich auch: Dass es nicht mit = geht.
Bis demnächst
Matthias
@@Matthias Apsel
Naja, bei 3 Gleichheitszeichen passt’s noch in eine.
Ich bin auf deine Lösung gespannt.
Sei ϕ der an u anliegende Innenwinkel des Dreiecks. Dann ist sin ϕ = q / u und cos ϕ = q / v, also u = q / sin ϕ und v = q / cos ϕ.
$$\frac{u^2 v^2}{u^2 + v^2} = \frac{\frac{q^2}{\sin^2 \varphi} \cdot \frac{q^2}{\cos^2 \varphi}}{\frac{q^2}{\sin^2 \varphi} + \frac{q^2}{\cos^2 \varphi}} = \frac{q^4}{q^2 \left( \cos^2 \varphi + \sin^2 \varphi \right)} = q^2$$
LLAP 🖖
Hallo Gunnar Bittersmann,
Ja. Es lässt sich in eine Zeile quetschen. Von netter Aufbereitung hätst du wohl nichts? ;-)
Bis demnächst
Matthias
@@Matthias Apsel
Von netter Aufbereitung hätst du wohl nichts? ;-)
Doch. Erstt hatte ich im LaTeX \phi durch \varphi ersetzt, nun auch noch im Text φ (U+03C6 GREEK SMALL LETTER PHI) durch ϕ (U+03D5 GREEK PHI SYMBOL). Wenngleich die Glyphen für die beiden Zeichen in manchen Schriftarten vertauscht sind.
LLAP 🖖
Hallo Gunnar Bittersmann,
Mit netter Aufbereitung meinte ich eher:
Sei u der an A liegende Hypotenusenabschnitt.
Dann gilt:
$$\sin \alpha = \frac{q}{u}, \sin \beta = \frac{q}{v} = \cos \alpha$$
letzeres weil α und β Komplementärwinkel sind.
Weiter ist
$$\begin{align}
\sin ^2 \alpha + cos ^2 \beta & = 1
\frac{q^2}{u^2} + \frac{q^2}{v^2} & = 1
\end{align}$$
Die Umformungsschritte mag jeder selbst vornehmen.
Bis demnächst
Matthias
@@Matthias Apsel
Mit netter Aufbereitung meinte ich eher:
Sei u der an A liegende Hypotenusenabschnitt.
Eckpunkte brauchst du nicht, sie kommen im Folgenden nicht vor.
Dann gilt:
$$\sin \alpha = \frac{q}{u}$$
Sag ich doch. Über Benennungen werden wir nicht streiten.
$$\sin \beta = \frac{q}{v} = \cos \alpha$$
letzeres weil α und β Komplementärwinkel sind.
β brauchst du nicht. cos α = q / v folgt direkt aus der Beziehung von Ankathete und Hypothenuse.
Weiter ist
$$\sin ^2 \alpha + cos ^2 \beta = 1$$
Den Pythagoras hab ich als bekannt vorausgesetzt. Die Beziehung hatte ich stillschweigend bei der letzten Umformung angewandt.
$$\frac{q^2}{u^2} + \frac{q^2}{v^2} = 1$$
Die Umformungsschritte mag jeder selbst vornehmen.
Ich hatte mich diesmal dafür entschieden, von $$\frac{u^2 v^2}{u^2 + v^2}$$ auszugehen und das so umzuformen, dass am Ende _q_² dasteht.
Wenngleich der Weg, von einer Binsenweisheit auszugehen und diese so umzuformen, dass die gesuchte Gleichung rauskommt, schon elegant ist.
LLAP 🖖
Hallo Gunnar Bittersmann,
Sei u der an A liegende Hypotenusenabschnitt.
Eckpunkte brauchst du nicht, sie kommen im Folgenden nicht vor.
Naja, der gemeine Schüler geht von dem aus, was gegeben ist und da sind α und β zuerst mal die Winkel im Dreieck ABC.
$$\sin \beta = \frac{q}{v} = \cos \alpha$$
letzeres weil α und β Komplementärwinkel sind.
β brauchst du nicht. cos α = q / v folgt direkt aus der Beziehung von Ankathete und Hypothenuse.
Ja. Aber siehe oben.
Und noch ein Klugschiss hintendran: In Kathete und Hypotenuse ist jeweils nur ein h. ;-)
Bis demnächst
Matthias
Hallo Matthias Apsel,
Und noch ein Klugschiss hintendran: In Kathete und Hypotenuse ist jeweils nur ein h. ;-)
Ich musste auch viele dieser Falschschreibungen korrigieren ;-) Wer im Glashaus sitzt …
Bis demnächst
Matthias
@@Matthias Apsel
Und noch ein Klugschiss hintendran: In Kathete und Hypotenuse ist jeweils nur ein h. ;-)
Ich musste auch viele dieser Falschschreibungen korrigieren ;-) Wer im Glashaus sitzt …
Wir sollten es dem ollen Pythagoras gleichtun und griechisch schreiben; τ und θ sind vermutlich nicht so leicht zu verwechseln wie t und th.
LLAP 🖖
Hallo,
Und noch ein Klugschiss hintendran: In Kathete und Hypotenuse ist jeweils nur ein h. ;-)
erstaunlich, ich hätte jetzt auch ziemlich überzeugt behauptet, dass sich diese längste Seite des Dreiecks nicht nur vorn, sondern auch in der Mitte mit h schreibt. Wahrscheinlich habe ich das auch schon oft so geschrieben.
Wer im Glashaus sitzt …
... sollte sich nur im Dunkeln ausziehen. ;-)
Ciao,
Martin
@@Gunnar Bittersmann
$$u^2 = \frac{a^2 \left( a^2 + b^2 \right)}{\left( a + b \right)^2}$$
Analog:
$$v^2 = \frac{b^2 \left( a^2 + b^2 \right)}{\left( a + b \right)^2}$$
Daraus sieht man, dass
$$\frac{u}{v} = \frac{a}{b}$$
Wie kriegt man das auch ohne Rechnung (d.h. auch ohne Winkelfunktionen) raus?
LLAP 🖖
Hallo Gunnar Bittersmann,
$$\frac{u}{v} = \frac{a}{b}$$
Falls u der an B grenzende Hypotenusenabschnitt ist.
Wie kriegt man das auch ohne Rechnung (d.h. auch ohne Winkelfunktionen) raus?
Der Punkt Q des Quadrates teilt das Dreieck ABC in zwei Teildreiecke, AQC und QBC.
Betrachtet man AQ und QB als Grundseiten, haben beide Dreiecke dieselbe Höhe h. Es gilt
$$\begin {align}
A_{AQC} = \frac{1}{2} vh\
A_{QBC} = \frac{1}{2} uh
\end {align}
$$
Außerdem lassen sich auch die Seiten a bzw. b als Grundseiten auffassen; dann haben beide Dreiecke die Höhe q. Es gilt:
$$\begin {align}
A_{AQC} = \frac{1}{2} bq\
A_{QBC} = \frac{1}{2} aq
\end {align}
$$
Folglich gilt:
$$\frac{A_{QBC}}{A_{AQC}} = \frac {\frac{1}{2} uh}{\frac{1}{2} vh} = \frac {\frac{1}{2} aq}{\frac{1}{2} bq}$$
Kürzen. Fertig.
Bis demnächst
Matthias
@@Matthias Apsel
Kürzen. Fertig.
Sehr nett.
Das war das Stück, das mir fehlte. Nun geht die Frühstückspausenaufgabe geometrisch.
Dazu errichten wir in B die Senkrechte zu AB; der darauf im Abstand v von B liegende Punkt auf der C gegenüberliegenden Seite sei S. Dessen Abstand von Q sei w.
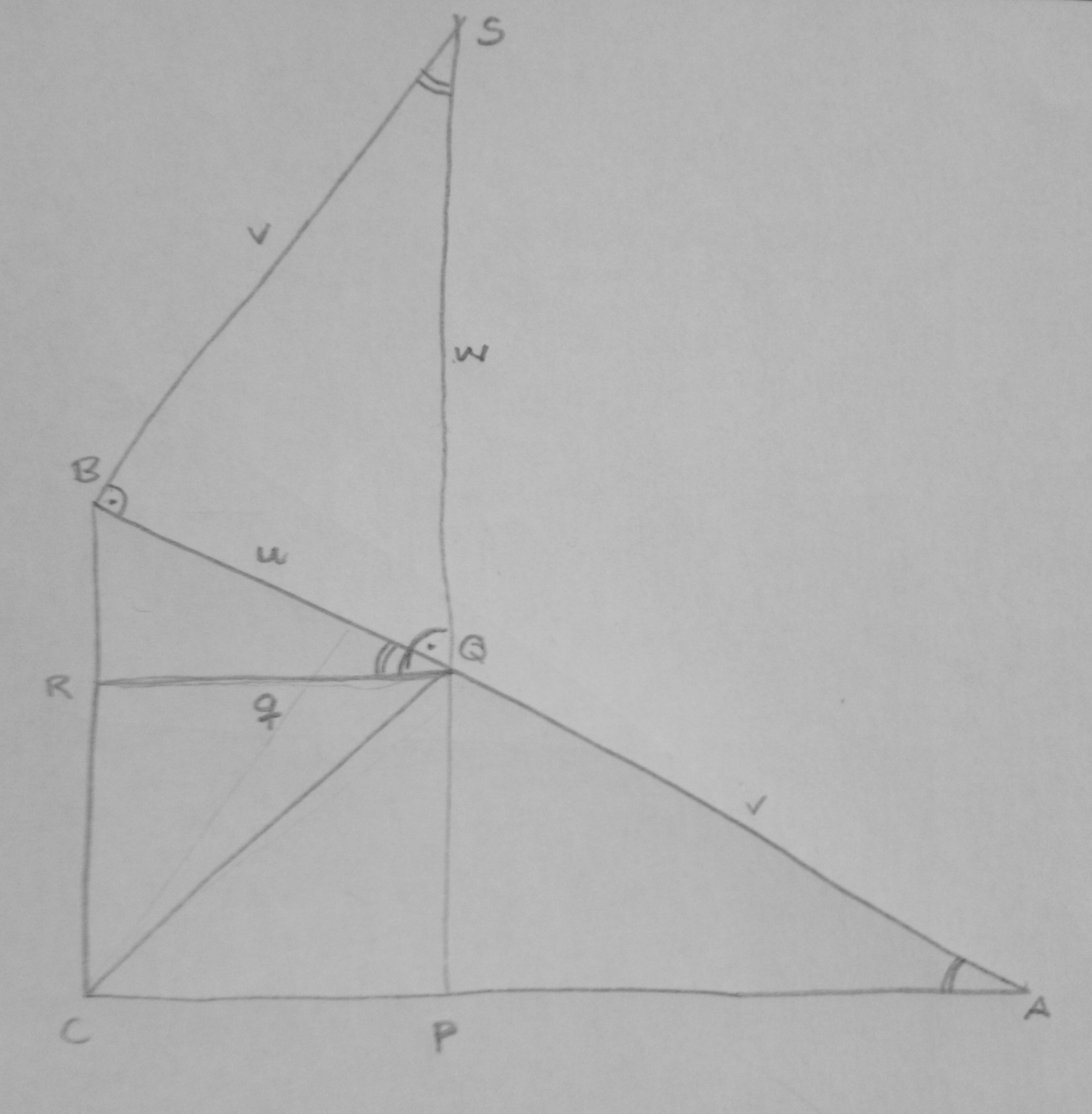
Aus der Rechtwinklichkeit und a / b = u / v folgt die Ähnlichkeit der Dreiecke ABC und QSB; sie stimmen also in den Winkeln überein. Daraus folgt, dass ∠RQS ein rechter ist.
Nun dieselbe Überlegung wie bei dir: Der Flächeninhalt des Dreieck QSB ergibt sich einerseits aus ½uv, andererseits aus ½qw.
Also ist u²v² = q²w² = q²(u² + v²). Da isser wieder, der gute alte Pythagoras.
LLAP 🖖
Na immerhin hab ich diesmal relativ zügig die Lösung gefunden. Zumindest für q und auch den algebraischen Nachweis für das Flächenverhältnis.
Die geometrische Überlegung mach ich jetzt und frage einstweilen: Sollte man seine Lösung verdeckt an den Aufgabensteller einsenden? Oder stellen wir uns einfach hin, sagen "haps" - äh - „hab's“ und glauben uns das? :)
Edit: Done - allerdings schaffe ich sowas leider doch nicht mehr in 2 Minuten. Es waren 5-10 (einiges davon ging zum sauberen Zeichnen drauf...). Aber vielleicht komme ich wieder auf das Tempo aus Studienzeiten, wenn Matthias fleißig weitere Aufgaben stellt.
Schade nur, dass außer Gunnar und mir keiner geantwortet hat. Alle noch im Bett vom Freitagabendbesäufnis?
Rolf
Strahlensatz anwenden, Verhältnisse von a:b und den Seiten eines der kleinen Dreiecke bilden, dann lässt sich das schön auflösen.
So richtig Lob erbitte ich mir allerdings für die Fähigkeit, NoScript so weit zu brinden dass es mich das Bild sehen ließ ;-)
@@encoder
Strahlensatz anwenden, Verhältnisse von a:b und den Seiten eines der kleinen Dreiecke bilden, dann lässt sich das schön auflösen.
Stimmt, so geht’s auch. Das ist vielleicht auch Matthias’ Straight-forwards-Lösung?
LLAP 🖖
Hallo Gunnar Bittersmann,
Stimmt, so geht’s auch. Das ist vielleicht auch Matthias’ Straight-forwards-Lösung?
Ja.
Bis demnächst
Matthias
Wie habt ihr es denn gemacht?
@@encoder
Wie habt ihr es denn gemacht?
Das Wochenende ist noch nicht vorbei.
LLAP 🖖
Ich habe es so wie du gemacht.
Hallo Gunnar Bittersmann,
Strahlensatz anwenden
Stimmt, so geht’s auch. Das ist vielleicht auch Matthias’ Straight-forwards-Lösung?
wobei ich nicht an den Strahlensatz gedacht habe, sondern
$$\tan \beta = \frac{b}{a} = \frac{q}{a-q} $$
was auf dasselbe hinausläuft.
Bis demnächst
Matthias
Hallo encoder,
So richtig Lob erbitte ich mir allerdings für die Fähigkeit, NoScript so weit zu brinden dass es mich das Bild sehen ließ ;-)
Dir ist schon aufgefallen, dass es nicht einfach nur ein Bild ist?
Bis demnächst
Matthias
Dir ist schon aufgefallen, dass es nicht einfach nur ein Bild ist?
Ja, dachte mir dann schon dass das kein pures Bild ist.
Meinte nur, Scripte die von wilden Buchstabenkombinationen kommen lass ich normalerweise nicht zu. Da hattest du als bekannter Name aus diesem Forum einen Bonus :-)