Mathematik zu Pfingsten

[Gunnar Bittersmann]

@@Matthias Apsel

So hab ich’s gemacht: Dreieck so in Koordinatensystem, dass die Eckpunkte A(−1, 0), B(1, 0) und C(0, √3) sind; der gesuchte Punkt ist P(0, a).

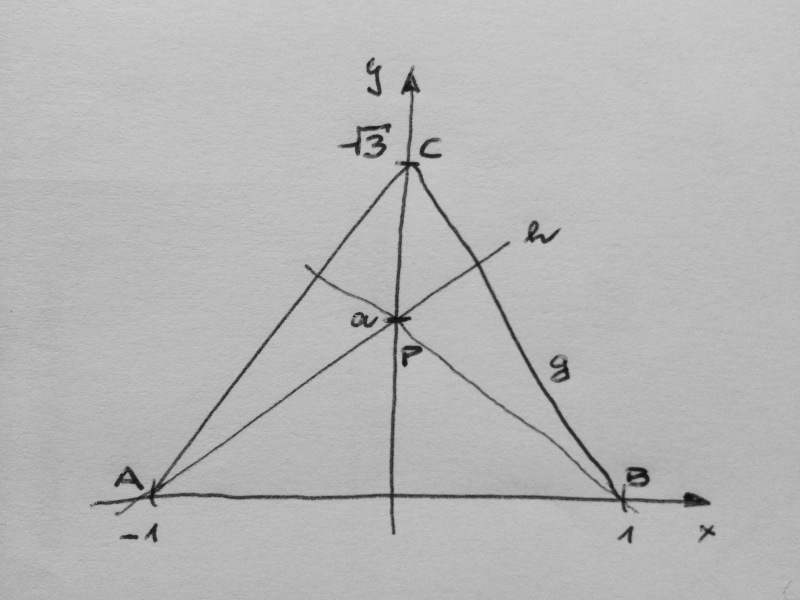
Die Gerade AP hat die Gleichung y = (1 + x) a.
Die Gerade BC hat die Gleichung y = (1 − x) √3.

Ermittlung des Flächeninhalts des Drachenvierecks über die x-Koordinate des Schnittpunkts der beiden Geraden:

$$\begin{align} \left( 1 + x\right ) a &= \left( 1 - x \right) \sqrt 3 \ x &= \frac{\sqrt 3 - a}{\sqrt 3 + a} \end{align}$$

$$A_{\text{Drachen}} = \left( \sqrt 3 - a \right) x = \frac{\left( \sqrt 3 - a \right)^2}{\sqrt 3 + a}$$

Wir bestimmen nun a so, dass der Flächeninhalt des Drachenvierecks ein Drittel des Flächeninhalts des Dreiecks ABP (welcher a beträgt) ist:

$$\begin{align} \frac{\left( \sqrt 3 - a \right)^2}{\sqrt 3 + a} &= \frac{a}{3} \ \tfrac{9}{2} - \tfrac{7}{2} \sqrt 3 , a + a^2 &= 0 \ a &= \tfrac{1}{2} \sqrt 3 \end{align}$$

(Die andere Lösung der quadratischen Gleichung entfällt, da der Punkt außerhalb des Dreiecks ABC wäre.)

Es ist also $$A_{ABC} = \sqrt 3$$ und $$A_{ABP} = \tfrac{1}{2} \sqrt 3$$ und $$A_{\text{Drachen}} = \tfrac{1}{6} \sqrt 3$$.

Jetzt ist noch zu prüfen, ob die beiden seitlichen Dreiecke ebensogroß wie das Drachenviereck sind. Deren Flächeninhalt ergibt sich aus

$$\tfrac{1}{2} \left( A_{ABC} - A_{ABP} - A_{\text{Drachen}} \right) = \tfrac{1}{2} \left( \sqrt 3 - \tfrac{1}{2} \sqrt 3 - \tfrac{1}{6} \sqrt 3 \right) = \tfrac{1}{6} \sqrt 3$$

---

Ich hatte micht auch gefragt: Und wie geht’s nun geometrisch, ohne Rechnen? Rolf b lässt mich vor Scham in den Erdboden versinken.

LLAP 🖖