Mathematik zum Start ins Wochenende

[Gunnar Bittersmann]

@@Matthias Apsel

Gegeben ist ein Körper (schräg abgeschnittenes Prisma) wie folgt: Auf einer dreieckigen Grundfläche stehen die Seitenkanten senkrecht. Zwei der Seitenkanten haben die Höhe h, die dritte ist doppelt so hoch. Gesucht ist das Volumen.

Lässt sich das auch verallgemeinern, zum Beispiel auf Seitenkanten, die nicht das Doppelte von einander sind, drei unterschiedlich lange Seitenkanten, Seitenkanten, die nicht senkrecht auf der Grundfläche stehen, n-Ecke …

Zweimal Höhe h₁, dritte h₂

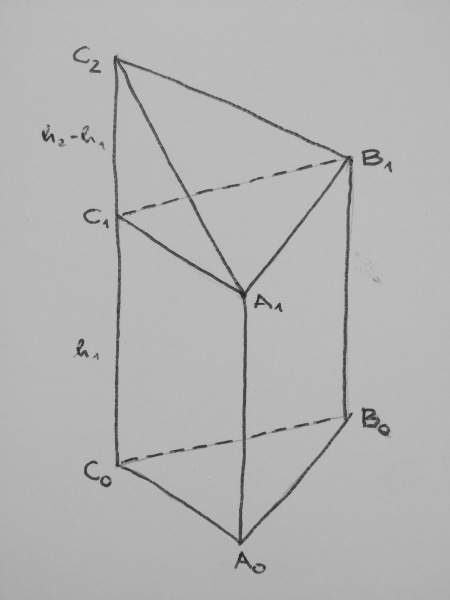
Fall 1: h₂ > h₁

Wir zerlegen den Körper in das Prisma A₀B₀C₀A₁B₁C₁ der Höhe h₁ und die Pyramide A₁B₁C₁C₂ der Höhe h₂ − h₁:

Das Volumen ist:

$$V = A_G h_1 + \frac{1}{3} A_G \left( h_2 - h_1 \right) = A_G \frac{ 2h_1 + h_2}{3}$$

Fall 2: h₂ < h₁

Hier wird eine Pyramide der Höhe h₁ − h₂ vom Prisma der Höhe h₁ weggeschnitten. (ohne Bild)

$$V = A_G h_1 - \frac{1}{3} A_G \left( h_1 - h_2 \right) = A_G \frac{ 2h_1 + h_2}{3}$$

Fall 3: h₂ = h₁

Wie man leicht sieht (wirklich!), gilt die Formel fürs Volumen auch dann.

Das Volumen des Körpers ist das Produkt aus der Grundfläche und dem Mittelwert der Höhen.

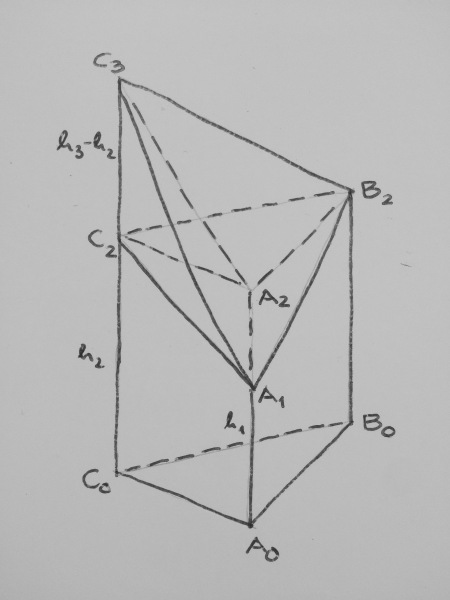
Drei unterschiedliche Höhen h₁, h₂, h₃

O.B.d.A. h₁ < h₂ < h₃

Wir zerlegen den Körper in den Körper A₀B₀C₀A₁B₂C₂ und die Pyramide A₁B₂C₂C₃:

Für das Volumen des Körpers A₀B₀C₀A₁B₂C₂ gilt (s.o., Fall 2):

$$V_K = A_G \frac{h_1 + 2 h_2}{3}$$

A₂ sei der Punkt über A₀ in der Höhe h₂. Wir betrachten kurzzeitig mal B₂C₂C₃ als Grundfläche der Pyramide (die ja ein Tetraeder ist). Jetzt kommt Cavalieri ins Spiel: Die Pyramide A₁B₂C₂C₃ hat dasselbe Volumen wie die Pyramide A₂B₂C₂C₃.

Dieses beträgt (jetzt wieder A₂B₂C₂ als Grundfläche):

$$V_P = \frac{1}{3} A_G \left( h_3 - h_2 \right)$$

Zusammenaddiert:

$$V = V_K + V_P = A_G \frac{h_1 + h_2 + h_3}{3}$$

Auch hier: Das Volumen des Körpers ist das Produkt aus der Grundfläche und dem Mittelwert der Höhen.

n-Eck als Grundfläche

Es liegt die Vermutung nahe, dass die Beziehung auch für beliebige n-Ecke als Grundfläche gilt.

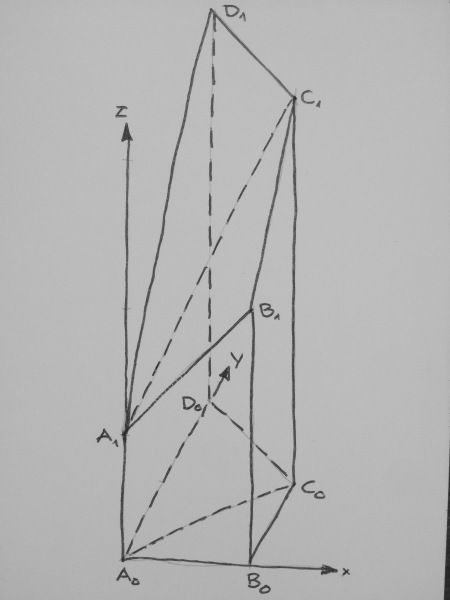
Wir wählen als Grundfläche das Viereck mit den Eckpunkten A₀(0, 0, 0), B₀(1, 0, 0), C₀(1, 1, 0), D₀(0, 2, 0). Deren Größe ist ³⁄₂.

Oben sei der Körper durch die Ebene z = x + y + 1 begrenzt.

Durch Einsetzen der Werte für x und y in die Ebenengleichung erhält man die Koordinaten der oberen Eckpunkte:
A₁(0, 0, 1), B₁(1, 0, 2), C₁(1, 1, 3), D₁(0, 2, 3).

Wenn unsere Vermutung stimmt, wäre das Volumen

$$V = A_G \frac{h_1 + h_2 + h_3 + h_4}{4} = \frac{3}{2} \cdot \frac{1 + 2 + 3 + 3}{4} = \frac{27}{8}$$

Wir zerlegen den Körper in zwei mit dreieckiger Grundfläche A₀B₀C₀A₁B₁C₁ (Fläche: ½) und C₀D₀A₀C₁D₁A₁ (Fläche: 1), für die wir die Formel zur Berechnung des Volumens ja kennen:

$$V = \frac{1}{2} \cdot \frac{1 + 2 + 3}{3} + 1 \cdot \frac{3 + 3 + 1}{3} = 1 + \frac{7}{3} = \frac{10}{3}$$

Das war dann wohl nichts mit unserer Vermutung. Die Beziehung gilt für dreieckige Grundflächen, nicht aber allgemein für n-Ecke.

LLAP 🖖