noch mehr Mathematik zum Wochenende – Lösung

[Gunnar Bittersmann]

@@Gunnar Bittersmann

Einen anderen Weg ist @ottogal gegangen: Man nimmt an, dass die Lösung 7 ist und beweist das.

Augenmaß anhand einer Skizze oder GeoGebra – wie man auf die 7 kommt, ist wie beim tapferem Schneiderlein egal, wenn denn der Beweis geführt wird.

@ottogal hatte aus demselben Gleichungssystem über das Additionstheorem $$\arcsin x + \arcsin y = \arcsin \left( x \sqrt{1 - y^2} + y \sqrt{1 - x^2} \right)$$
(Was es nicht alles gibt!) die Gültigkeit gezeigt.

Geht auch anders: Das Gleichungssystem brauchen wir nicht. Wir sortieren die Pizzastücken etwas anders: 7, 2, 11. Und wir müssen sie gar nicht halbieren.

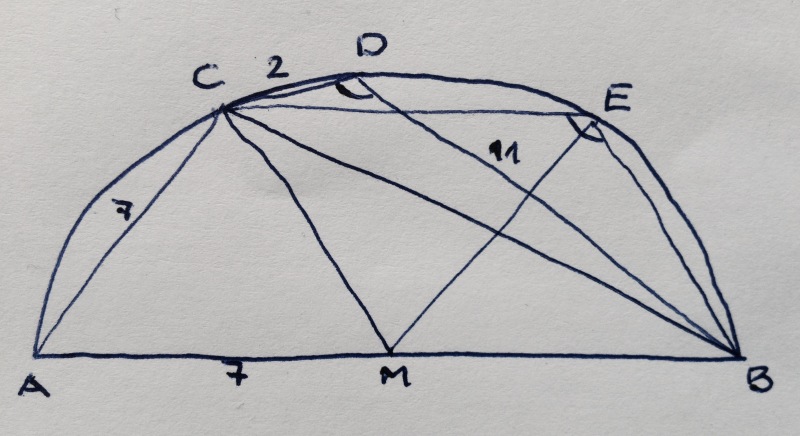
AB ist Durchmesser des Kreises mit Radius 7. Wir drehen den Spieß um und wählen C so auf der Peripherie, dass AC = 7 (das Dreieck AMC also gleichseitig ist); D so auf der Peripherie, dass CD = 2. Zu zeigen ist nun, dass dann DB = 11 ist.

Dazu wählen wir E so auf der Peripherie, dass die Dreiecke CME und MBE ebenfalls gleichseitig sind.

∠BDC und ∠BEC sind Peripheriewinkel über derselben Sehne CB, also beide jeweils ⅔π = 120° groß. Nach Pythagoras ist CB = 7√3.

Cosinussatz in Dreieck CBD:

CB² = CD² + DB² − 2 CD DB cos⅔π
7² ⋅ 3 = 2² + DB² − 2 ⋅ 2 ⋅ DB ⋅ (−½)
   147 = 4 + DB² + 2 DB
     0 = DB² + 2 DB − 143
    DB = −1 ± √144
    DB = 11, q.e.d

LLAP 🖖