Bei @Five_Triangles eine Aufgabe von Catriona Shearer gefunden, die sich als Wochenendknobelei ganz nett macht:

Die Zahlen geben die Flächeninhalte der jeweiligen Quadrate an. Wie groß ist die Differenz der Flächeninhalte der farblich markierten Dreiecke?
Erwähnte ich schon, dass man das ohne Pythagoras lösen sollte?
Und wie sie so schön schreiben, kann man die Zeichnung weiter ausmelken:
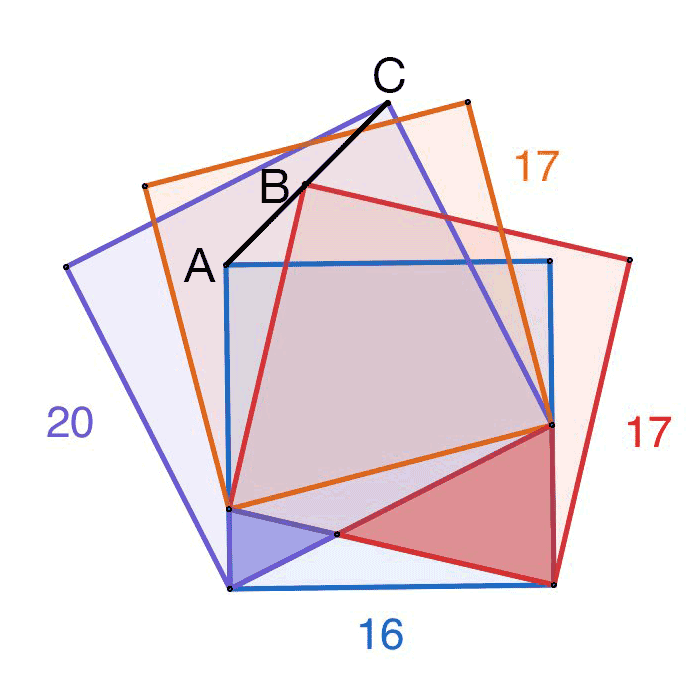
Zeige, dass A, B und C auf einer Linie liegen, und berechne das Verhältnis AB : BC.
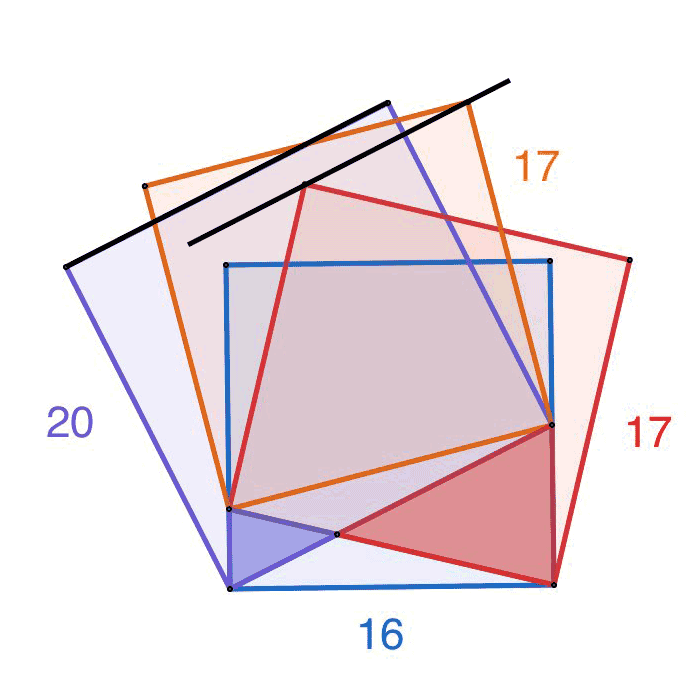
Zeige, dass die markierte Quadratseite und die eingezeichnete Linie durch die zwei Eckpunkte parallel sind.
LLAP 🖖
--
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann
„Wer durch Wissen und Erfahrung der Klügere ist, der sollte nicht nachgeben. Und nicht aufgeben.“ —Kurt Weidemann


