Mathematik zum Dienstagnachmittag - meine Lösung

[Rolf B]

Hallo,

mein Weg ging etwas anders, und zuerst auch VIEL mühsamer. Darum ist mein Bild ziemlich wüst geworden. Im Verlauf der Diskussion ging mir ein Kronleuchter auf...

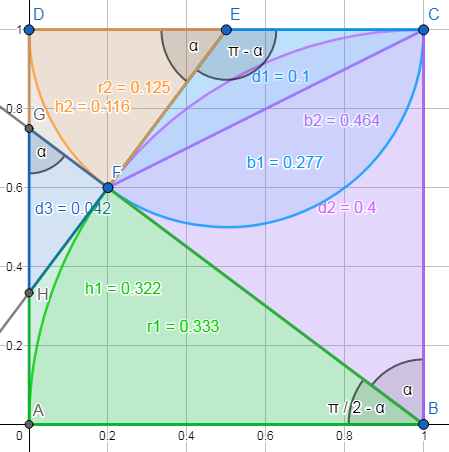
Im ersten Versuch hatte ich das Dreiech HFG sowie die beiden "Mützen" auf dem orangen und grünen Kreissektor separat berechnet. Wie deppert...

Wie Ottogal schon nachgewiesen hat, hat BCEF die halbe Quadratfläche. Das Fünfeck ABFED links davon also auch.

Ziehe ich vom Fünfeck den orangen und grünen Kreissektor ab, erhalte ich den Schwanz. Fertig. Nix mit Dreiecken und Mützen.

Addiere ich den blauen und lilafarbenen Kreissektor, erhalte ich das Drachenviereck plus den Bauch - weil der Bauchteil des Fisches die Überlappung darstellt und damit zweimal in diese Addition eingeht.

Für den Fisch bekommt man also: A(ABFED) - A(Orange) - A(Grün) + A(Blau) + A(Lila) - A(BCEF).

Fünfeck und Drache sind gleich groß, subtrahieren sich also weg. Ich brauche nur die Flächen der vier Kreissektoren.

Ich verwende die "Standard-Kreissektorformel". Ein Kreissektor mit Radius r und Öffnungswinkel φ hat die Fläche: $$A(S_{r, φ}) = \frac{1}{2}φ r^2$$.^[1]

Damit ergibt sich A(Lila) - A(Grün) = $$\frac{1}{2}\alpha 1^2 - \frac{1}{2}(\frac{\pi}{2} - \alpha) 1^2 = \frac{1}{2}\alpha - \frac{\pi}{4} + \frac{1}{2}\alpha = \alpha - \frac{\pi}{4} $$

Und A(Blau) - A(Orange) = $$\frac{1}{2}(\pi-\alpha) \frac{1}{2}^2 - \frac{1}{2}\alpha \frac{1}{2}^2 = \frac{\pi}{8} - \frac{\alpha}{8} - \frac{\alpha}{8} = \frac{\pi}{8} - \frac{\alpha}{4} $$

In Summe $$A(Fisch) = \alpha - \frac{\pi}{4} + \frac{\pi}{8} - \frac{\alpha}{4} = \frac{3}{4}\alpha - \frac{\pi}{8} $$

Mein α ist doppelt so groß wie Ottogals, darum hat er drei Halbe und ich drei Viertel.

Für α gibt's mehrere Quellen. Einmal natürlich wie Ottogal über $$2\arctan{\frac{1}{2}}$$; aber α findet sich auch in HFG, und da kennen wir aus Gunnars Aufgabe die Seitenverhältnisse. Gegenkathete zu Hypotenuse ist 4:5, also $$\alpha = \arcsin\frac{4}{5}$$

$$A(Fisch) = \frac{3}{4}\arcsin\frac{4}{5} - \frac{\pi}{8} \approx 0{,}30277$$

Rolf

---

1. Was für ein Dreck - das kleine Phi gibt's in drei Glyphen: U+03C6 φ, U+03D5 ϕ und U+0278 ɸ. Das Foren CSS setzt mir "Menlo", "Monaco" und "Consolas" als Font-Family ein, aber Consolas hat die Glyphen für φ und ϕ vertauscht. Im Editor sehe ich den linken der zwei als Kreis mit senkrechtem Strich drin. Alle anderen Windows-Fonts zeigen es andersrum, und die Grafiktafel der Wikipedia ebenso 😟 ↩︎