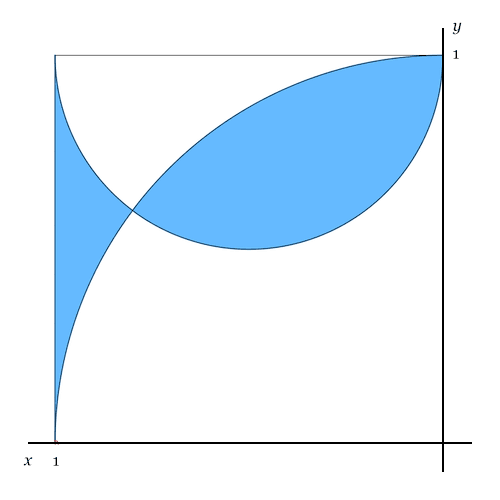
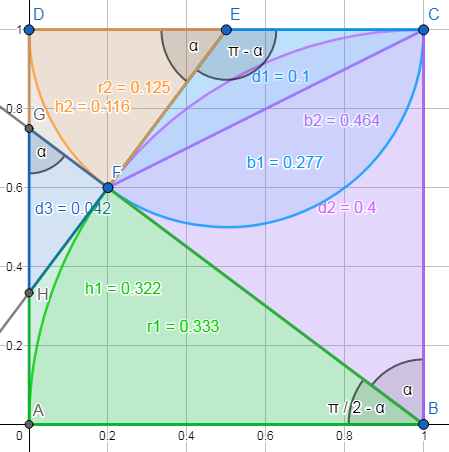
In ein Quadrat sind ein Halbkreis und ein Viertelkreis einbeschrieben, so dass sich folgende Fisch-Figur ergibt:
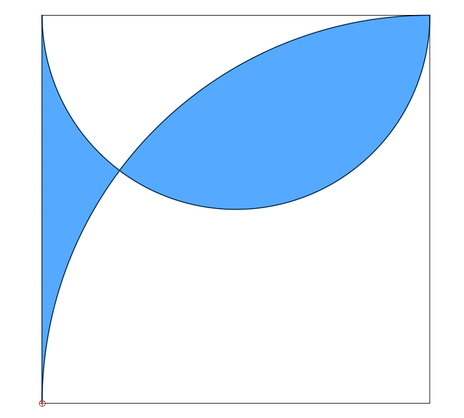
Man berechne den Anteil der blauen Fisch-Fläche an der Quadratfläche.
Guten Morgen Mathefans,
die Aufgabe ist jetzt fast eine Woche alt - ich verrate mal meine Lösung:
(1)
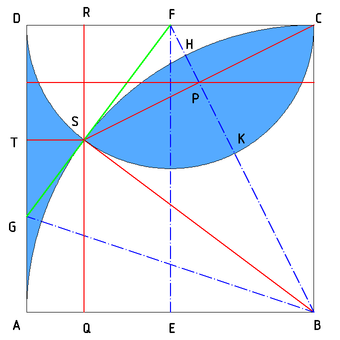
O.b.d.A habe das Quadrat $$ABCD$$ die Seitenlänge $$1$$.
Der Viertelkreis hat den Mittelpunkt $$B$$ und den Radius $$1$$.
Der Mittelpunkt des Halbkreises ist der Mittelpunkt $$F$$ der Seite $$CD$$, sein Radius ist $$\frac{1}{2}$$.
Der Schnittpunkt der beiden Kreisbögen ist $$S$$.
Wir nehmen für Winkelwerte stets das Bogenmaß; der Vollwinkel hat also den Wert $$2\pi$$.
(2)
$$BCFS$$ ist ein Drachenviereck mit der Symmetrieachse $$BF$$ (denn $$BS$$ und $$BC$$ bzw. $$FS$$ und $$FC$$ sind als Kreisradien jeweils gleich lang).
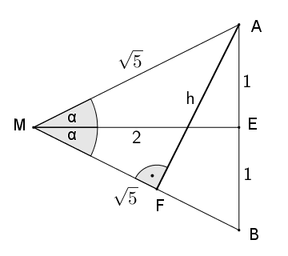
Das Drachenviereck hat den Flächeninhalt $$\frac{1}{2}$$, denn es ist flächengleich zum Rechteck $$EBCF$$ (da die rechtwinkligen Dreiecke $$BFS$$ und $$FBE$$ nach dem SWS-Satz kongruent sind).
(3)
Wir müssen natürlich Sektorflächen berechnen. Dies wird durch die Verwendung des Bogenmaßes für Winkel besonders einfach.
Ein Sektor habe den Radius $$r$$ und den halben Öffnungswinkel $$\phi$$.
Seine Fläche verhält sich zur Fläche des Vollkreises wie sein Öffnungswinkel zum Vollwinkel:
$$\frac{A_{Sektor}}{\pi r^2} = \frac{2 \phi}{2 \pi} = \frac{\phi}{\pi}$$
So erhält man die einfache Formel
|$$A_{Sektor} = \phi \cdot r^2$$
(4)
Der Winkel $$\alpha = \angle CBF$$ kommt noch an anderen Stellen vor:
auch die Winkel $$\angle FBS$$, $$\angle FCS$$ und $$\angle FSC$$ haben den Wert $$\alpha$$, und es folgt $$\angle DFS = 2\alpha$$.
Wegen $$\tan \alpha = \frac{FC}{BC} = \frac{1}{2}$$ ist
|$$\alpha = \arctan$$ $$\frac{1}{2} = 0,46365$$
(Dies ist die einzige Stelle, an der wir die Trigonometrie bemühen müssen!)
Wir werden eine Formel für den gesuchten Flächeninhalt des Fisches herleiten; dabei verwenden wir durchgängig die Konstante $$\alpha$$. Erst am Schluss setzen wir den obigen numerischen Wert ein, um einen Zahlenwert für den gesuchten Flächenanteil zu erhalten.
(5)
Zunächst berechnen wir den Flächeninhalt des Schwanzstücks $$DAS$$ des Fisches links von $$S$$.
Wir erhalten $$A_{Schwanz}$$, indem wir von der Quadratfläche $$1$$ das Drachenviereck $$A_{BCFS} = \frac{1}{2}$$ sowie die beiden Sektorflächen $$A_1 = A_{BSA}$$ und $$A_2 = A_{FDS}$$ subtrahieren.
Der Sektor $$BSA$$ hat den Radius $$1$$ und den halben Öffnungswinkel
$$(\frac{\pi}{2}$$$$-2\alpha):2=\frac{1}{4}\pi-\alpha$$, somit nach (2) die Fläche
$$A_1 = (\frac{1}{4}$$$$\pi-\alpha) \cdot 1^2 = \frac{1}{4}\pi-\alpha$$
Der Sektor $$FDS$$ hat den Radius $$\frac{1}{2}$$ und den halben Öffnungswinkel $$\alpha$$ und daher die Fläche
$$A_2 = \alpha \cdot $$$$(\frac{1}{2})^2 = \frac{1}{4}\alpha$$
Der Fischschwanz hat folglich die Fläche
$$A_{Schwanz} = 1-\frac{1}{2}$$$$-A_1-A_2 = \frac{1}{2}-(\frac{1}{4}\pi-\alpha)-\frac{1}{4}\alpha$$
also
|$$A_{Schwanz} = \frac{1}{2}$$$$-\frac{1}{4}\pi+\frac{3}{4}\alpha$$
Zwischen-Bemerkung:
Um nun den Körper des Fisches zu bekommen, könnte man die Flächen der beiden Segmente $$SCH$$ und $$CSK$$ berechnen (als Differenz jeweils einer Sektor- und einer Dreiecksfläche) und addieren. So ging mein erster Lösungsweg.
Dann jedoch hat mir Rolf am Mittwochmorgen ein Licht aufgesetzt - als er vom Herausrechnen von gewissen Überlappungen sprach.
Das brachte mich schließlich zu den folgenden Überlegungen.
(6)
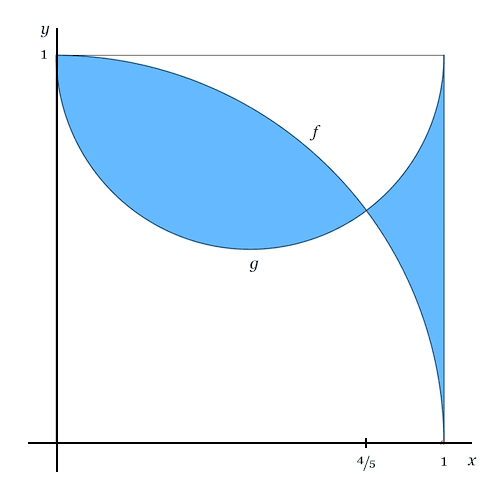
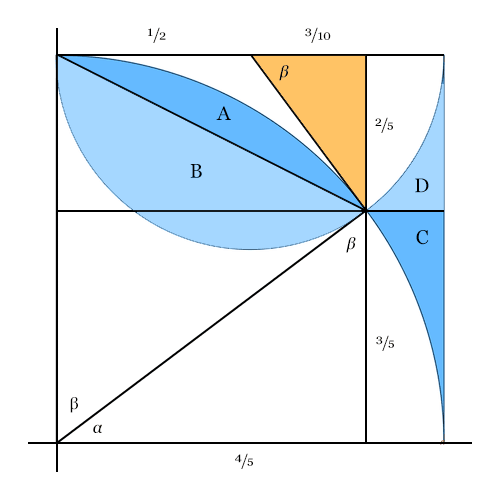
Addiert man die Flächen des Halbkreises und des Viertelkreises, so erhält man die Quadratfläche abzüglich des Fischschwanzes, aber zuzüglich des Fischkörpers, der - wegen der Überlappung - zweimal in die Summe eingeht (doppelt schraffiert):
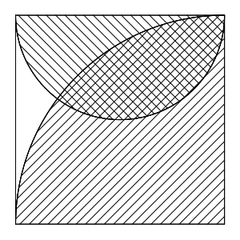
Nun meine Idee:
Wir addieren noch zweimal den Fischschwanz - einmal, um die Lücke zu füllen, und das zweite mal, um ihn (wie den Körper) zweimal in die Summe eingehen zu lassen (doppelt schraffiert)!
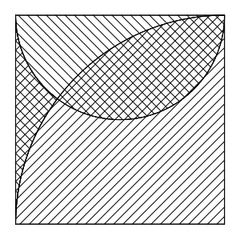
Subtrahiert man nun von all dem einmal die Quadratfläche, bleibt genau die Fläche des Fisches übrig!
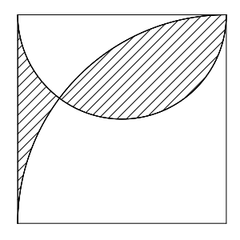
Die Fischfläche berechnet sich demnach wie folgt:
$$A_{Fisch} = A_{Viertelkreis} + A_{Halbkreis} + 2 \cdot A_{Schwanz} - A_{Quadrat}$$
$$= \frac{1}{4}$$ $$\pi \cdot 1^2 + \frac{1}{2}\pi \cdot (\frac{1}{2})^2 + 2 \cdot (\frac{1}{2} - \frac{1}{4}\pi + \frac{3}{4}\alpha) - 1$$
$$= \frac{3}{8}$$ $$\pi + 1 - \frac{1}{2}\pi + \frac{3}{2}\alpha - 1$$
also
$$A_{Fisch} = \frac{3}{2}$$ $$\alpha - \frac{1}{8}\pi$$
Mit dem Wert von $$\alpha$$ aus (3) erhalten wir das
Ergebnis:
|$$A_{Fisch} = \frac{3}{2}$$ $$\arctan{\frac{1}{2}} - \frac{1}{8}\pi$$
Das ist etwa $$0,30277$$; der Fisch nimmt also etwa 30,28% der Quadratfläche ein.
Fazit: Wenn mans mal gefunden hat, ist es immer einfach...
Euch einen guten Start in die Woche!
ottogal
ottogal
Rolf B
Gunnar Bittersmann
Tabellenkalk
