nicht angemeldet
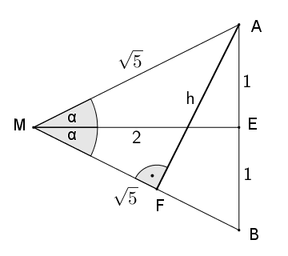
Um zu bestätigen, dass Rolfs Ergebnis identisch mit meinem ist, hab ich die folgende Aussage direkt bewiesen:
Behauptung:
$$arcsin{\frac{4}{5}}$$$$ = 2 \cdot arctan{\frac{1}{2}}$$
Beweis:
Wir setzen $$\alpha$$$$= arctan{\frac{1}{2}}$$. Dann ist zu zeigen: $$\sin 2\alpha$$$$=\frac{4}{5}$$.
Nach Pythagoras ist $$MB^2 = 2^2+1^2$$, also $$MB=\sqrt 5$$.
Somit ist $$\sin 2\alpha$$$$=\frac{AF}{AM}=\frac{h}{\sqrt 5}$$
Um $$h$$ zu bestimmen, schreiben wir den Flächeninhalt $$A_{ABM}$$ auf zwei Arten:
$$A_{ABM}$$$$=\frac{1}{2} \cdot AB \cdot ME=\frac{1}{2} \cdot 2 \cdot 2=2$$
$$A_{ABM}$$$$=\frac{1}{2} \cdot \sqrt 5 \cdot h$$
Gleichsetzen liefert $$h=\frac{4}{\sqrt 5}$$, und damit folgt $$\sin 2\alpha$$$$=\frac{4}{5}$$.
Rolf B
Gunnar Bittersmann
Tabellenkalk