Mathematik zum Dienstagnachmittag

[Gunnar Bittersmann]

@@Gunnar Bittersmann

So, nach unzähligen Versuchen und am Ende ein bisschen reverse engineering, um auch noch den letzten Vorzeichenfehler zu finden, hab ich das nun auch geschafft.

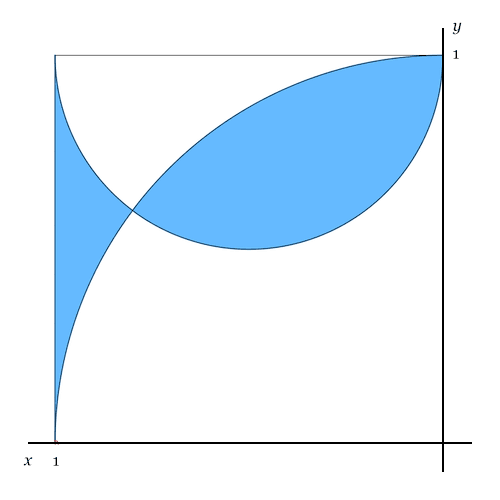
Und zwar so: Quadrat (o.B.d.A. Seitenlänge 1) so in ein Koordinatensystem gelegt, dass der große Viertelkreis seinen Mittelpunkt in O hat und der kleine Halbkreis seinen Mittelpunkt in (½, 1).

Wenn wir die x-Achse (aus lauter Gewohnheit) nach rechts zeigen lassen wollen, spiegeln wir:

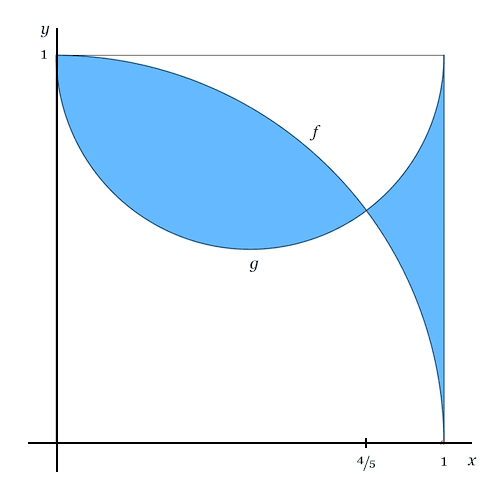
Der große Viertelkreis hat die Kreisgleichung x² + y² = 1; der kleine Halbkreis (x − ½)² + (y − 1)² = ¼. Sie werden also durch die Funktionen

$$y = f(x) = \sqrt{1 - x^2}
y = g(x) = 1 - \sqrt{\tfrac{1}{4} - \left( x - \tfrac{1}{2} \right)^2} = 1 - \sqrt{x \left( 1 - x \right)}$$

beschrieben. (Die Vorzeichen vor den Wurzeln ergeben sich daraus, dass wir beim großen Vierteilkreis den oberen Teil des Kreises brauchen; beim kleinen Halbkreis den unteren Teil.)

Zur Bestimmung der Fläche müssen wir nun die Differenz f(x) − g(x) integrieren; aber nicht über den Schnittpunkt hinweg! (Der – wie man durch Gleichsetzen f(x) = g(x), Quadrieren, Isolieren der Wurzel, nochmaliges Quadrieren leicht herausbekommt – bei x = ⅘ liegt.)

$$A = \left| \ \int_0^\frac{4}{5} \left( f(x) - g(x) \right) \mathrm dx \ \right|

• \left| \ \int_\frac{4}{5}^1 \left( f(x) - g(x) \right) \mathrm dx \ \right| = \int_0^\frac{4}{5} \left( f(x) - g(x) \right) \mathrm dx

• \int_\frac{4}{5}^1 \left( f(x) - g(x) \right) \mathrm dx$$

Die Integrale hatte ich ja schon verraten; meine Rechnung sah dann so aus:

Ergebnis: $$A= \tfrac{1}{4} \pi - \tfrac{3}{4} \arcsin \tfrac{3}{5}$$. Puh!

Wie Rolf sagte: „schön mühsam“.

LLAP 🖖